Planimetria Blue: Okrąg o promieniu 6 opisano na czworokącie ABCD. Boki AD i DC mają równe długości, a kąt ABC ma miarę 120 stopni. Oblicz pole tego czworokąta, jeśli stosunek pól trójkątów ABD i BCD jest równy 2:1.

zawodus: Samodzielnej pracy troszkę włóż blue Zapewne jesteś sympatyczną i uroczą dziewczyną potrafiącą zrobić chociaż rysunek tutaj do zadania

Blue: Właśnie szczerze mówiąc, nigdy za bardzo nie ogarniałam, jak tutaj na forum się rysuje. : ) Zawodus, bardzo mi miło, że tak sądzisz, myślałam, że tutaj na forum wszyscy mnie nienawidzą...

Mila: Dobrze przepisałaś treść?

zawodus: Dlaczego? chyba nie dlatego, że pragniesz się nauczyć matematyki? Jeśli to zadanie nie na jutro to mogę ci pomóc Chyba, że napiszesz na gadu (8959267), to może znajdę chwilkę później i pomogę

Blue: Mila na pewno wszystko jest dobrze przepisane Zawodus, to zadanie nie na jutro, jest z gwiazdką, więc wątpię, abym sama je rozwiązała. Jak będziesz miał rozwiązanie, to daj mi znać

zawodus: Mam rozwiązanie Ale brak czasu na jego umieszczenie

Blue: To poczekam do jutra, czy tam pojutrza, na razie się zbieram , a jutro mnie praktycznie cały dzień nie będzie, więc masz czas

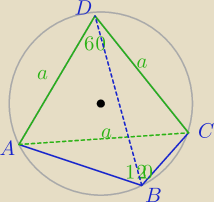
Mila: Podpowiedź. ΔACD− Δrównoboczny

Eta:

Eta: Witaj Mila Czy też taką masz odpowiedź:

	243√3
P(ABCD)=
	7

Mila: Witam , serdecznie Eto. Taką samą mam odpowiedź.

zawodus: Witam Mila i Eta

	81√3
A mnie wyszło
	2

zawodus: Czyli chyba coś zepsułem

Eta: Witaj zawodus A no, a no ......... 2:1 ( to szukaj błędu

Mila: Po wskazówce Blue na pewno rozwiąże. Witaj zawodus

zawodus: Nie chce mi się szukać błędu może jutro

Maslanek: Okrąg ten jest opisany także na tójkącie ADC skąd łatwo z tw. sinusów policzyć długość a.

a
	=2R.
sin60

Potem jakiś szybkie twierdzenie cosinusów dla ustalenia stosunku odległości AB i BC. I tw. cosinusów dla trójkąta ABC w celu ustalenia jednej z nich

Blue: A idzie to zrobić bez tych twierdzeń Bo w książce to zadanie jest jeszcze przed tymi twierdzeniami? Jak inaczej wyliczyć to a

Blue: sorry, tego drugiego znaku zapytania nie powinno być : Bo w książce to zadanie jest jeszcze przed tymi twierdzeniami ; p

zawodus: będzie ciężko, ale pomyślę

zawodus: ile u ciebie trwa rok szkolny?

Blue: 12 miesięcy haha ^^

zawodus: Sposób bez twierdzenia cosinusów jest, ale sporo liczenia Decyduj − albo uczysz się twierdzenia cosinusów (ewentualnie sinusów) albo jesteś skazana na rachunki (u mnie jakaś strona A5 pisana maczkiem )

Mila: R=6cm h_ΔACD=(6:2)*3=9

	a√3
h=
	2

	a√3
9=		⇔a=6√3
	2

Z porównania pól ΔABD i ΔBCD

1		1
	*|AB|*a*sinA=2*		|BC|*a*sinC
2		2

∡C=180^o−∡A, sin(180^o−∡A)=sinA⇒ |AB|=2*|BC| W ΔACB: z tw. cosinusów a²=(2|BC|)²+|BC|²−2*2|BC|²*cos 120^o

	−1
36*3=5|BC|2−4|BC|2*
	2

108=7|BC|²

	108
|BC|2=
	7

	1
PΔABC=		*2|BC|*|BC|*sin120o
	2

	√3		108		√3
PΔABC=|BC|2*		=		*
	2		7		2

	54√3
PΔABC=
	7

P_ABCD=P_ΔACD+P_ΔACB Dokoncz

Mila: To zadanie jest po partii materiału ze znajomością tw. sinusów ( to można tu ominąć) i tw. cosinusów.

Blue: a więc najpierw przerobię te twierdzenia, ale wydaje mi się to dziwne, bo to zadanie nie jest w tym temacie

Mila: Rozwiązujesz zadania ze zbioru dla klasy II?

Blue: tak, z książki dla klasy 2 , skąd wiesz?

Blue: Nie rozumiem, jak Ty wyliczyłaś tą wysokość... dlaczego 6:2*3

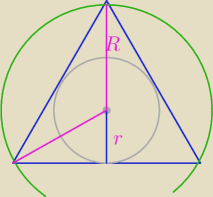
Mila: To wiadomości z Δ równobocznego. R=2r h=3r

	1
r=		h
	3

	2
R=		h
	3

Blue: No to teraz już wszystko jest jasne ! dzięki Mila, ale powiem Ci, że to zadanie jest skomplikowane, idzie się w nim pogubić

Mila: Nie jest trudne, jeśli porozwiązujesz trochę zadań, to będzie wtedy łatwe dla Ciebie. Z wysokością, to poziom GM. W LO mało czasu poświęca się na zadania z planimetrii i dlatego zapomniałaś trochę zależności.

H2O: Mógłby ktoś dokończyć to zadanie? Bardzo proszę