Funkcje wymierne ggg: Potrzebuję pomocy z tym zadaniem, a mianowicie nie tyle co z zadaniem, a z jego częścią. Nie umiem podać przedziałów monotoniczności tych funkcji. Proszę o wytłumaczenie i zrobienie po kolei np. jednej funkcji, a drugą postaram się zrobić analogicznie. A razie problemów zwrócę się o pomoc... Podaj przedzialy monotoniczności tych funkcji :

	x2 + x + 1
f(x) =
	x + 1

	−3x2 − 10x +9
g(x)=
	x2 + 2x − 3

Mila: Pochodne znasz?

Janek191:

	x2 + x + 1
f(x) =		; x ≠ − 1
	x + 1

Liczymy pochodną

	(2x + 1)*( x + 1) − ( x2 + x + 1)*1
f '(x) =		=
	( x + 1)2

	2 x2 + 2x + x + 1 − x2 − x − 1		x2 + 2x
=		=
	( x + 1)2		( x + 1)2

f '(x) > 0 ⇔ x² + 2x = x*( x + 2) >0 ⇔ x ∊ ( −∞ ; − 2 ) ∪ ( 0 ; + ∞ ) Funkcja rośnie w ( − ∞ ; − 2) ∪ ( 0 : + ∞), a maleje w ( − 2; − 1) ∪ ( − 1; 0 )

Janek191: f maleje w ( − 2; − 1) i w ( − 1; 0 )

Janek191: f rośnie w ( − ∞ ; − 2) i w ( 0 ; + ∞ )

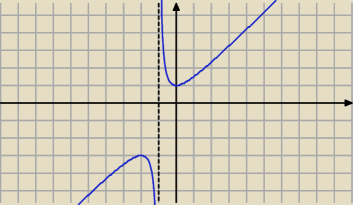
Bogdan: x ≠ −1 Nie stosuje się znaku sumy zbiorów ∪ w zapisie monotoniczności funkcji, bo zapis z takim znakiem może być błędny. Np. w tym Janek 191 zapisał: funkcja maleje w (−∞, −2)∪(0, +∞). Sprawdzamy to stwierdzenie zgodnie z definicją funkcji malejącej w określonym zbiorze.

	3
Weźmy x1 = −		, x2 = 0, mamy tu x2 − x1 > 0
	2

Zgodnie z definicją, funkcja jest malejąca w podanym przedziale, tu w (−∞, −2)∪(0, +∞), wtedy gdy dla dowolnych wartości x₁, x₂ z tego przedziału zachodzi f(x₂) − f(x₁) < 0.

	3		7		3
f(x1) = f(		) = −		, f(x2) = f(0) = 1, f(x2) − f(x1) = 1 − (−		) > 0
	2		2		2

co sugeruje, że funkcja jest rosnąca, a tak tu nie jest. Zapis f maleje w (−∞; −2) i w (0; +∞) też nie jest poprawny, spójnik i oznacza część wspólną zbiorów. Poprawny zapis to: funkcja maleje w (−∞, −2), (0, +∞).

ggg: Właśnie nie znam pochodnej... Dział ten jest przed pochodną...

ggg: Jaki jest inny sposób jeśli nie znam pochodnej?

ggg: Ale bardzo dziękuję za wyczerpującą odpowiedź pozdrawiam.