Planimetria Blue: Dany jest okrąg o promieniu 8. Cięciwa AB tego okręgu ma długość 4√7 i przecina średnicę PQ pod kątem prostym. Wyznacz sinus kąta ostrego czworokąta ABPQ i podaj przybliżoną miarę tego kąta .

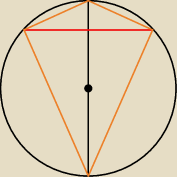
wredulus_pospolitus: chociaż rysunek został zrobiony a sinus którego kąta tego czworokąta ten czworokąt to jaka figura Czego się składa Znasz przekątne tego czworokąta, więc w czym problem

Blue: Zrobiłam rysunek, był jeszcze podpunkt a i go zrobiłam dobrze, ale nie wiem, jak wyliczyć tego sinusa...Kąt ostry jest przy wierzchołku P czy tam Q(zależy jak kto sobie oznaczy). A figura to deltoid of course

Blue: Problem w tym, że mam tutaj dwa trójkąty prostokątne, ale żaden z nich nie ma kąta ostrego, którego sinusa muszę wyliczyć. Te trójkąty mają tylko połowe tego kąta..

Janek191: 2r = r + x + ( r − x) = ( r + x) + ( r − x) Mamy( r + x)*( r − x) = ( 2√7)² = 4*7 = 28 więc ( 8 + x)*( 8 − x) = 28 64 − x² = 28 x² = 64 − 28 = 36 x = 6 ====

	2√7		2√7		√7		1
tg α =		=		=		⇒ tg2α =
	r + x		14		7		7

zatem

	2 tg α		2√77		√7
tg β = tg 2α =		=		=		≈ 0,8819
	1 − tg2α		1 − 17		3

β ≈ 41^o

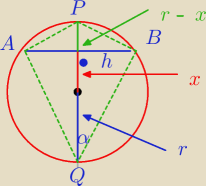
Janek191: h = 2√7 h² = ( r + x)*( r − x)

Blue: Dzięki Janek , ale my mieliśmy wyliczyć sinusa. Ale to nie szkodzi, bo już rozumiem, zupełnie zapomniałam o wzorze sin2α ^^

Janek191:

	√7
tg β =		⇒ b = √7 i a = 3 ⇒ c2 = a2 + b2 = 9 + 7 = 16 ⇒ c = 4
	3

	b		√7
sin β =		=		≈ 0,6614
	c		4

β ≈ 41^o25'

Janek191:

	√7
tg β =		⇒ b = √7 i a = 3 ⇒ c2 = a2 + b2 = 9 + 7 = 16 ⇒ c = 4
	3

	b		√7
sin β =		=		≈ 0,6614
	c		4

β ≈ 41^o25' czworokąt ( deltoid) APBQ.

Blue: Już nie musisz liczyć, zorientowałam się, jak to wyliczyć, gdy napisałeś wzór na tg2α i przypomniałam sobie wtedy , że jest też sin2α Dzięki za pomoc

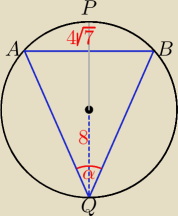
Bogdan: Nie ma tu czworokąta ABPQ, ale jest AQBP (to istotna różnica).

	4√7
W tym zadaniu nie ma co liczyć, stosujemy po prostu twierdzenie sinusów:		= 16,
	sinα

	4√7		4
stąd sinα =		=
	16		√7

pigor: ... lub jeśli |∡APB|=α= ? , to ze wzorów na pole czworokąta tu o prostopadłych przekątnych : PB²sinα = ¹₂*16*4√7 ⇒ (*) PB²sinα = 32√7, gdzie np. PB²= (8+6)²+(2√7²= 14*14+4*7= 32*7 ⇒ 32*7sinα= 32√7 ⇒ z (*) sinα= ¹₇√7 ≈ 0,3780 − szukany sinus kata ostrego , stąd α ≈ 22^o lub PB²= (8+2)²+(2√7²= 4*25+4*7= 32*4 ⇒ 32*4sinα= 32√7 ⇒ sinα= ¹₄√7 ≈ 0,6614 − szukany sinus kata ostrego , stąd α ≈ 41^o .

pigor: ..., tak tw. sinusów to jest to w tym zadaniu,

	√7
ale miało być ... sinα=		prawda ?Bogdanie
	4

Blue: ja tam wolę wykorzystać wzór na sin2α

Bogdan:

	√7
Tak pigor, oczywiście sinα =		.
	4

Do Blue − wyobraź sobie sytuację, w której dwóch kandydatów w procesie konkursowym do zajęcia jakiegoś istotnego dla nich miejsca (np. posady albo miejsca na studiach na obleganym kierunku) przedstawia swoje projekty. Osoba pierwsza prezentuje drogie i czasochłonne rozwiązanie, osoba druga tanie i proste. Kto otrzyma wymarzone miejsce? Po co wyznaczać sin2α, jeśli można od razu podać sinα.

Blue: oj, Bogdan może i tak, ale oba sposoby są dobrze

Blue: *dobre

Bogdan: Nieprawda, że oba sposoby są dobre. Można dojechać z Warszawy do Gdańska przez Zakopane i też powiemy, że dojechaliśmy. Dowolną drogę prawie każdy potrafi wskazać, ale najkrótszą i najprostszą już nie każdy.