blan blan: podaj przykład przepisu funkcji f takiej że całka od 0 do 5 z f(x) =0 i całka 2 do 3 f(x)=−3 Prośze o pomoc

Mila:

	1		5
1) f(x)=		(x−		)3
	2		2

₀∫⁵f(x) dx=0

blan: możesz wytumaczyc skąd tam do trzeciej i jedna druga ?

Godzio: ³ jest dlatego, żeby funkcja była nieparzysta (tzn. f(−x) = −f(x) ) dzięki temu całka na przedziale [−a,a] dla a ≥ 0 jest równa 0. My chcemy, żeby przedział był [0,5] więc przesuwamy sobie o

	5
		w prawo(to jest środek naszego przedziału).
	2

1
	podejrzewam jest do drugiego warunku, aby całka na [2,3] była równa −3 (dowolna liczba
2

przed funkcją nie wpływa na wartość pierwszej całki).

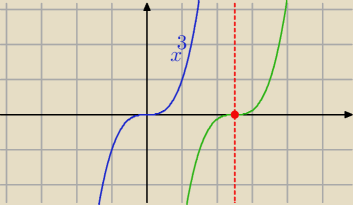
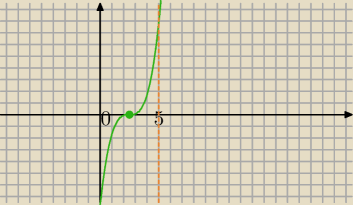
Mila: f(x)=x³ jest funkcją nieparzystą. (wykres symetryczny względem (0,0))

	5
Przesunęłąm o wektor [		,0] wtedy jest wzór :
	2

	5
f(x−		)+b⇔
	2

	5		5
g(x)=(x−		)3 wykres jest teraz symetryczny względem punktu(		,0)
	2		2

1
	przed wzorem spłaszcza wykres.
2