2 Zadania z prawdopodobieństwa temporary: Ktoś,coś? 1. Obsługa zapytania wymaga działania dwóch serwerów. Jeżeli awaryjność serwerów jest 0.02 i 0.04 dla każdego systemu z osobna, jaka jest awaryjność całego systemu, przy założeniu niezależności zdarzeń oraz założeniu, że jeżeli system pierwszy ulegnie awarii to prawdopodobieństwo awarii systemu drugiego wzrasta (względem sytuacji bez awarii) dwukrotnie. 2. Na serwerze czas obliczeń dany jest rozkładem o gęstości f(t)=2αte^−αt2 1_(0;∞) (t). Czasy obliczeń liczone są tylko dla zadań dłuższych od sekundy. Jak należy oszacować parametr α jeżeli wiemy, że ¹_e zadań dla których znamy czas obliczeń liczy się dłużej niż 3 sekundy.

temporary: Nikt nie jest na tyle odważny ?

Ada: Albo to jest bardzo proste, albo ja się bardzo nie znam (co jest zresztą bardzo prawdopodobne) 1. Jeżeli urządzenie potrzebuje dwóch to takie jak suma prawdopodobieństw (bo z zadania wynika, że są dwa serwery dwa muszą działać). 2. Czy nie wystarczy tej funkcji znormalizować

temporary: Można by prosić jakieś rozwiązanie z komentarzem do 2 zadania?

Ada: Nie umiesz normalizować funkcji gęstości prawdopodobieństwa ∫₀^∞ 2αt e^−αt2 dt = 1

temporary: Aaa, nigdy po prostu nie słyszałem, że ktoś to określał normalizowaniem

Ada: Aha

Trivial: Funkcja f(t) jest znormalizowanym rozkładem gęstości dla dowolnego α>0.

Trivial: A jeśli chodzi o zadanko pierwsze to jest bardzo dziwnie sformułowane (chodzi o te wzrosty prawdopodobieństwa drugiej awarii). Bez uwzględniania tych wzrostów, prawdopodobieństwo awarii wynosi: 1 − (1−0.02)*(1−0.04) = 5.92% Z uwzględnianiem wzrostów będzie gorzej, gdyż kolejność w której psują się serwery ma znaczenie.

Ada:

	1
No to kwantyl rzędu		jest równy 3.
	e

Ale ja się bardzo nie znam.

Trivial: Sposób na drugie zadanko, który ma szanse zadziałać. Zmodyfikować rozkład f(t) tak, aby nie uwzględniał czasów < 1s.

	⎧	βf(t) dla t > 1
f*(t) =	⎨
	⎩	0 w przeciwnym razie

	1
gdzie β =		= eα
	∫1∞ f(t)dt

Obliczamy prawdopodobieństwo:

	1
P[T > 3] = ∫3∞ βf(t)dt = βe−9α = e−8α =chcemy=
	e

	1
Zatem α =		.
	8

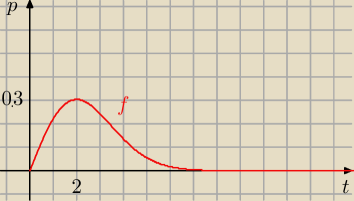
Trivial: A tutaj wykres gotowego rozkładu f.

temporary: Merci