odleglosc dwoch punktow 5-latek: Linie przerywana narysowalem nie dlatego ze to jest trojkat tylko dlatego zeby lepiej bylo widac do pisania odlegolsci punktow Definicja :Mowimy ze w zbiorze X okreslilismy odleglosc jezeli: Kazdej parze elementow tego zbioru przyporzadkowalismy dokladnie jedna liczbe nieujemna ktora nazwalismy odlegloscia pierwszego elementu od drugiego przy czym 1. a b nalezy do X to odleglosc a od b jest zerem wtedy i tylko wtedy gdy a=b 2. a,b nalezy do X to odleglosc a od b jest rowna odleglosci b do a 3. a,b nalezy do X to odleglosc od a do c nie jest wieksza od sumy odleglosci a od b i odleglosci b do c Teraz tak zgodnie z ta definicja (tak rozumiana odlegloscia w plaszcyznie ) mozemy zapisac tak AB<AC+CB BC<BA+AC CA<CB+BA co mozemy zapisac inaczej AB<AC+CB AB>AC−CB AB>CB−AC Nie rozumien dlaczego jest napisane (druga nierownosc AB>AC−CB mamy −BA<AC−BC ale BA=AB i to samo BC=CB wiec bedzie −AB<AC−CB to AB>−AC+CB to AB>CB−AC a jest odwrotnie AB>AC−CB

Maslanek: Bo oczywiście jest błąd . Chochliki się zdarzają Trzeba podchodzić odrobinę krytycznie

pigor: no bo widocznie na rysunku są długości AC > CB, a co do trzeciej nierówności, to byłaby zapisana wtedy, gdyby długości były takie CB >AC −−−−−−−−−−−−−−−−−−−−−−−−−−− można się tym nie przejmować i zapisywać moduł różnicy np.tak : |AC−CB|< AB< AC+CB lub |CB−AC|< AB< AC+CB . ...

5-latek: Witaj tak myslisz ? To w 3 nierownosci tez wychodzi ze jest blad BO potem (to rozumiem ) pisze tak : Liczby AC−CBi CB−AC sa liczbami przeciwnymi Jedna z nich wiec jest rowna |AC−CB| a druga −|AC−CB| zatem warunek AB>AC−CB i AB>CB−AC zapizsemy AB>|AC_CB| Jesli wiec punkty A b C nie sa wspoliniowe to zgodnie z naszym rozumawaniem prostej i odleglosci |AC−CB|<AB<AC+CB

5-latek: dziekuje pigor Pisalem swojego posta ale nie widzialem Twojego Nie ma tu nic o dlugosciach. PO prostu nie rozumien tego zapisu (moze on jest prawidlowy ) ze z drugiej nierownosci BC<BA+AC to wychodzi AB>AC−CB Ja po prostu tego nie rozumiem napisalem swoje obliczenia ale moze one sa zle . Wiec pytam na forum Wiec jesli mozesz to dokladniej wytlumaczyc to bede CI wdzieczny

5-latek: Chodzi o rozpisanie tej nierownisci BC<BA+AC do tej postaci AB>AC−CB

5-latek: jednak bym prosil o wskazanie miejsca gdzie robie ewentualnie blad z przy tym przekztalceniu nierownosci

Mila: AB<AC+CB , BC<BA+AC /−AC , CA<CB+BA /−CB co mozemy zapisac inaczej AB<AC+CB , BC−AC<AB , CA−CB<AB

5-latek: Wtedy mamy BC−AC<AB to AB>BC−AC i takze CA−CB<AB to AB>CA−CB Normalnie A ja tu kombinuje z wartosciami bezwzglednymi . dziekuje

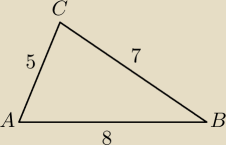
Mila: 8<5+7 8>7−5 8>5−7

5-latek: Rozumiem . Tutaj chodzilo oto zeby wykazac taka wlasnosc / W plaszcyznie jest okreslona odleglosc przyporzadkowujaca parze punktow X i Y liczbe ktora oznaczamy XY taka ze: punkty ABC nie sa wspoliniowe wtedy i tylko wtedy gdy |AC−CB|<AB<AC+CB (co faktycznie nazywamy nierownoscia trojkata .

Mila: Tu masz 3 punkty niewspółliniowe.

5-latek: Tak Milu wiem . Teraz jesli punkty sa wspoliniowe . Ale teraz bedzie latwiej bo AB=AC+CB lub AB=|AC−CB| Jeszce raz dziekuje