matematykaszkolna.pl
Oblicz pole nieograniczonej figury Kamil: Oblicz pole nieograniczonej figury płaskiej: A={(x,y): 0<x; 0<y<x/(3x)}
29 cze 17:34
Ada: Liczysz granice. Tak jak dla funkcji jednej zmiennej.
29 cze 18:25
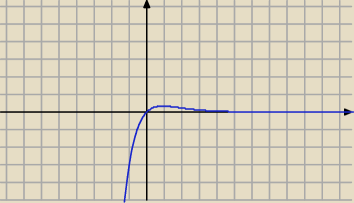
Mila: rysunek
 x 
y=
 3x 
 x 1 
0∫∞(
) dx=0∫∞(x*(
)x) dx=...
 3x 3 
 1 1 
 1 
(
)x)
 3 
 
[x=u, dx=du , dv=(
)x) dx, v=∫(
)x) dx=
]
 3 3 ln(1/3) 
 
 1 
(
)x)
 3 
 
 1 
(
)x)
 3 
 
..=x*
−∫
dx=
 ln(1/3) ln(1/3) 
 
 1 
(
)x)
 3 
 
 1 
(
)x)
 3 
 
=[x*
−
]0∞=
 ln(1/3) ln2(1/3) 
 x 1 
=[
−
]0∞==
 3x*(ln(1)−ln(3)) 3x*(ln(1)−ln(3))2 
 ε 1 ε 1 
=limε→∞[{
−
]−limε→0[{
−
]=
 −3ε*ln(3) 3ε*ln2(3) −3ε*ln(3) 3ε*ln2(3) 
 1 1 
=0−0−0+
=
 ln2(3) ln2(3) 
29 cze 23:37