Planimetria Blue: Na okręgu o promieniu 3 opisano trójkąt równoramienny o kącie między ramionami równym 120 stopni. Oblicz długość boków tego trójkąta. Zrobiłam rysunek i próbuję to liczyć z zależności trójkąta prostokątnego o kątach 90,60, 30, ale wychodzi mi po ułożeniu równania 0=0...

	1		a√3
przyjmuję sobie za		a = x+3 i dalej wyznaczam a i		. I potem z twierdzenia
	2		2

pitagorasa, ale wychodzi 0=0. Ma ktoś jakiś pomysł?

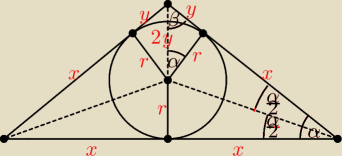
Bogdan: Szkic: Środek okręgu wpisanego to .... α = 30^o, β = 60^o, r = 3 y√3 = 3 ⇒ y = √3

	√3
x + y = x√3 ⇒ √3 = x√3 − x ⇒ x =
	√3 − 1

Długości boków: 2x, x+y, x+y

Blue: a skąd Ci się wzięło to x+y = x√3

Blue: Robię to innym sposobem, ale też mi wyszło, już rozumiem wszystko, dzięki