 hah
A więc do rzeczy − zaczynam planimetrię (jest to dział, z którego jestem najsłabsza, więc
pewnie będę Was dużo męczyć za co z góry przepraszam).
Mam problem z tym zadaniem:
Dany jest ośmiokąt foremny o boku długości 1 . Oblicz długość okręgu oraz pole koła:
a) opisanego na tym ośmiokącie
b) wpisanego w ten ośmiokąt.
Nie mam pojęcia jak obliczyć promień tego okręgu, kąt środkowy ma 45 stopni... ale co z tym
zrobić?
hah
A więc do rzeczy − zaczynam planimetrię (jest to dział, z którego jestem najsłabsza, więc
pewnie będę Was dużo męczyć za co z góry przepraszam).
Mam problem z tym zadaniem:
Dany jest ośmiokąt foremny o boku długości 1 . Oblicz długość okręgu oraz pole koła:
a) opisanego na tym ośmiokącie
b) wpisanego w ten ośmiokąt.
Nie mam pojęcia jak obliczyć promień tego okręgu, kąt środkowy ma 45 stopni... ale co z tym
zrobić?
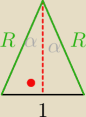 Nie wiem czy dobrze kombinuję ale to jest okrąg opisany w tym przypadku.
wiesz że 2α=45o
i teraz twierdzenie cosinusów może ?
Nie wiem czy dobrze kombinuję ale to jest okrąg opisany w tym przypadku.
wiesz że 2α=45o
i teraz twierdzenie cosinusów może ?
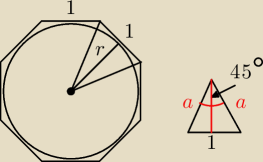 360:8=45
czyli mamy trójkąt równoramienny o kącie między ramionami 45o
Można np z twierdzenia Carnota policzyć długość "a"
potem pitagoras
360:8=45
czyli mamy trójkąt równoramienny o kącie między ramionami 45o
Można np z twierdzenia Carnota policzyć długość "a"
potem pitagoras  Zapewne jest znacznie prostsze rozwiązania, ale o tej porze myślę jeszcze na poziomie 25%
Zapewne jest znacznie prostsze rozwiązania, ale o tej porze myślę jeszcze na poziomie 25% 


| 1 | ||
P= | a2sin45 | |
| 2 |
| 1 | ||
P= | h | |
| 2 |
| 1 | ||
( | )2+h2=a2 | |
| 2 |


| √2 | ||
z tego układu wyszło mi, że a= | , ale to chyba jest źle... | |
| 4 |

 Proponuję uogólnić zagadnienie do postaci: wyznaczyć długość promienia okręgu opisanego
i długość promienia okręgu wpisanego w n−kąt foremny o boku długości a.
Proponuję uogólnić zagadnienie do postaci: wyznaczyć długość promienia okręgu opisanego
i długość promienia okręgu wpisanego w n−kąt foremny o boku długości a.
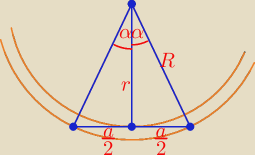 a − długość boku n−kąta foremnego
a − długość boku n−kąta foremnego
| 2π | π | |||
2α = | ⇒ α = | |||
| n | n |
| a | ||
R i r wyznaczamy rozwiązując trójkąt prostokątny o bokach: | , r, R i kącie ostrym α: | |
| 2 |
| a | a | |||||||||||||||||||||
R = | , r = | |||||||||||||||||||||
|
|
| π | √2 − √2 | |||
Dla n = 8: α = | = 22,5o, sin22,5o = | , tg22,5o = √2 − 1 | ||
| 8 | 2 |
| √2 + √2 | ||
Dodatkowo podaję wartości: cos22,5o = | , ctg22,5o = √2 + 1 | |
| 2 |



| (2+√2)√2−√2 | ||
wyszło mi | , ale w odpowiedziach mam inaczej, tzn mówię o długości okręgu | |
| 2 |

 Wystarczy zatem Pitagoras i musi być ok )
Wystarczy zatem Pitagoras i musi być ok )


