Wykres setaRDG: Jak zaznaczyć na osi x²+y²=6 , y=x² I jakie są punkty wspólne ? Potrafię to sobie wyobrazić bo pierwsze to jest równanie okręgu a 2 to jest parabola ale nie wiem jakie mogą byc punkty wspólne

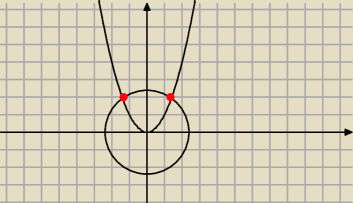
razor: punkty wspólne: podstawiam y = x² do równania okręgu y+y²=6 y²+y−6 = 0 (y+3)(y−2) = 0 y = −3 lub y = 2 podstawiając y = −3 do równania okręgu otrzymujemy sprzeczność dla y = 2 x² = 2 x = √2 lub x = −√2 nasze szukane punkty wspólne mają współrzędne (−√2,2) lub (√2,2)

Saizou :

setaRDG: A powiedzcie mi prosze jak by to wyglądało gdybym chciał to zapisać w postaci całki oznaczonej ∫((y²+y−6)−x²)dx ? ? Cos takiego czy inaczej ?

setaRDG: I kolejne 2 równania y=x⁴−1 , y=0 . A w takich równaniach punkty wspolne Podstawiamy do pierwszego za y=0 0=x⁴−1 (x²−1)(x²+1)=0 (x−1)(x+1)(x²+1)=0 Dobrze to robię

Mila: 1) Do zadania 23:19 napisz od początku treść. 2) 23:23 dalej tak: x−1=0 lub x+1=0 lub x²+1=0 x=1 lub x=−1 , brak rozwiązań bo x²+1>0

setaRDG: Do 1 zadania Mam policzyć pole powstałe w wyniku naszkicowania dwóch równań x²+y²=6 , y=x² Koledzy mi już pomogli i narysowali wykres . A teraz mam problem zapisania tego jako calke . Bo równanie x²+y²=6 bd ograniczać od góry a y=x² bd ograniczać od dołu i chodzi mi tylko o zapis

Mila: Pole ograniczone krzywymi?

setaRDG: Tak

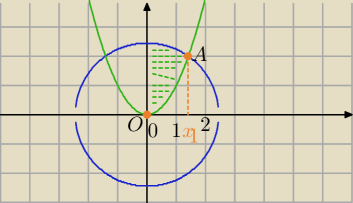
Mila: Rozważymy pole w I ćwiartce,( korzystamy z symetrii.) x²+y²=6 y²=6−x² y=√6−x² Razor obliczył wsp. punktów przecięcia x₀=0, x₁=√2 P=2*₀∫^√2 ( √6−x²−x²) dx ∫( √6−x²−x²) dx=∫√6−x²dx−∫x² dx=.. pierwsza całka z wzoru, ( masz?) , druga prosta

setaRDG:

	1
kolejne pytanie Mam 3 proste y=		, y=0, x>3
	(x−3)2

Jak bd wygladał wykres i jakie są punkty wspolne 3 i +∞ ?

setaRDG: yhy rozumię Ale też mogę całkę wziąśc od razu od przedziału −√2 do √2

Mila:

	a2		x		x
∫√a2−x2 dx=		arcsin		+		√a2−x2+C
	2		a		2

	6		x		x
∫√6−x2dx=		arcsin		+		√6−x2=
	2		√6		2

	x		x
=3 arcsin		+		√6−x2
	√6		2

setaRDG: Tak mam ten wzór podany tylko , że wynik ma się równać arcsin(x)/(a)

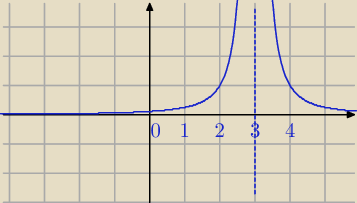
Mila: 0:09 tak . Tu będzie całka niewłaściwa. Granice od 3 do ∞.

	−1		−1		−1
3∫∞U{1}{(x−3)2 dx=[		]3∞= limε→∞(		)−limε→3+(		)=0+∞
	x−3		ε−3		ε−3

całka rozbiezna pospawdzaj znaki, bo już śpię. Dobranoc

setaRDG: Tak calka rozbieżna , dziękuję i Dobranoc