Zamiana całki podwójnej do współrzędnych polarnych. Magdalena: Oto całka: (₋√₂∫⁰) dy (₋y∫√4−y²) xy dx zapis taki: przed całką dolna granica, po całce górna granica całkowania. Mam problem z przetransformowaniem tego na polar coordinate'y. Wydaje mi się, ze rysunek wygląda tak: http://i.imgur.com/FLKHjs3.png ponieważ: y=−x −√2<=y<=0 x²+y² = 4 (r=2) Szare linie to obszar. Problem w tym, ze nie mam pojęcia jak to zapisać w coordinate'ach polarnych. Proszę o pomoc z wytłumaczeniem. Nie rozumiem tego, ponieważ w jednym miejscu obszar jest ograniczony prostą, więc nie mogę chyba tego zapisać jak całka (0∫2)dr (π∫7/8π)dφ

Krzysiek: x=√4−y² czyli x≥0 więc zły rysunek po drugie dolna granica to x=−y więc obszar zaczyna się od tej prostej a nie kończy się na niej. jak poprawisz rysunek to wtedy łatwo wyznaczysz kąt.

Ada: 1. Proszę używać polskiego nazewnictwa, współrzędne biegunowe. 2. Jak są one zdefiniowane? Bo moja wiedza mówi mi, że nie tak jak to jest zapisane, tylko: x = r cosφ y = r sinφ wtedy jakobian przekształcenia jest równy: J = r Jakobian to wyznacznik macierzy Jacobiego: http://pl.wikipedia.org/wiki/Macierz_Jacobiego 3. Ograniczasz zmienne, dla twojego przypadku: r ∊ (0, √2) Dalej jaki obszar jest podany w zadaniu od tego zależą ograniczenia na φ

Magdalena: Krzysiek, dzieki, ale nie rozumiem. x = √4−y², to prawda ale x² = 4 − y² x² + y² = 4 a więc kółko o promieniu 2 o starcie w punkcie (0,0). Jak to mozliwe ze X'y > 0?

Krzysiek: x=√4−y² a x²+y²=4 to nie to samo. x=√4−y² dla x<0 to równanie jest sprzeczne

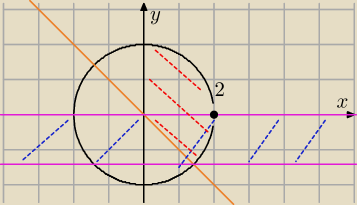
Ada: Ok, nie ogarnęłam zapisu. Przepraszam. x∊(−y, √4−y²) − czerwono ograniczenia x y∊(−√2,0) − niebiesko ograniczenia y

	7
Wychodzi wycinek koła dla φ∊(		π, 2π) r∊(0,2)
	8

I = ∫₀² dr ∫_7/8π ^2π r³ sinφ cosφ dφ

Krzysiek: tylko,że 'czerwone ograniczenie' jest źle oznaczone.

Ada: Czemu

Krzysiek: bo sięga do pomarańczowej prostej a nie zatrzymuje się na prostej: x=0

Ada: Kiedy się zatrzymuje Jak rozważasz y=√4−x² to oznacza górną połowę koła, a teraz przekręć układ współrzędnych Nie obejmuję ujemnych x−sów, I i IV ćwierci x jest dodatnie.

Magdalena: Ada, źle. tam gdzie są czerwone I niebieskie linie, powinno być zamalowane. wynik poprawny to ₀∫² dr _−π/4 ∫⁰ dφ

Krzysiek: tylko,że to z prawej strony ogranicza nasz obszar a z lewej x=−y więc 'x' może być ujemny...

Magdalena: no tak, czyli odpowiedź którą zapisałam jest poprawna, tak?

Krzysiek: brakuje u Ciebie funkcji podcałkowej.

Ada: Krzysiek chyba nie rozumiem.

	−π		7
Tak, Magdaleno tylko, że kąt		jest równoważny kątowi		π, kąt 0 kątowi 2π.
	4		8

Krzysiek: Ada, a jak byś narysowała taki obszar: −y≤x≤2−y ? to co by ograniczało obszar z lewej strony? prosta x=0 ? nie,7/8π tylko −π/4+2π=7π/4

Magdalena: nie brakuje funckji podcałkowej, po prostu jej nie zapisałam bo uznałam ze jest tak banalna ze nie ma po co zapisywać. Cieszę się natomiast, że doszłam do wyniku. Temat można zamknąć.