zadanie nr 4 5-latek: Czy stosunek przecinania sie prostych jest 1. zwrotny ( a wiec czy a nierownolegle a ) 2. symetryczny (a wiec czy a nierownolegle b to b nierownolegle a) 3.Przechodni (a wiec czy a nierownolegle b i b nierownolegle c to a nierownolegle c ) Odpowiedz dokladnie uzasadnij Czy jest symetryczny . tak jest symetryczny .Dlatego ze kiedy sie dwie proste przecinaja to maja jeden wspolny punkt Zwrotnym chyba nie bedzie bo a moze byc tylko rownolegla do a

zawodus: Podstawowy warunek: mówimy o prostych na płaszczyźnie czy w przestrzeni?

5-latek: Witam serdecznie Oczywiscie mowimy o plasczyznie. O przestrzeni porozmawiamy pozniej (pod koniec roku ) Bo stosunek rownoleglosci jest zwrotny

zawodus: a jest równoległa do a, zatem nie możemy mówić tutaj o zwrotności wg mnie

5-latek: czyli tak jak myslalem A teraz stosunek przechodniosci przecinania sie prostych ta wlasnosc stosunku rownoleglosci jest opisana tak Jesli aIIb i bIIc to albo jest a=c albo proste a i c jako dwie proste rownolegle do tej samej prostej b nie moga nalezec do tego samego peku. Wiec czesc wspolna a i c = zbior pusty Poniewaz a=c lub czesc wspolna a i c = zbior pusty zatem aIIc czyli aIIb i bIIc to aIIc Jak teraz wzorujac sie na tym udowodnic ze stosunk przecinania sie prostych(czyli stosunek nierownoleglosci) jest przechodni

Maslanek: Nie jest przechodni zdaje się Jeżeli b przecina a i a jest równoległa do c, to b również przecina c. Stąd i z równoległości nie zachodzi implikacja a~b ∧ b~c ⇒ a~c. Więc relacja nie jest przechodnia.

5-latek: Witaj. W tamtym zadaniu miales racje . Nalezalo skorzystac z odleglosci i nierownosci trojkata . Tutaj chyba bedzie jednak przechodnia (nie bede sie w tej chwili upieral przy tym )

5-latek: Musze jeszce dobrze poczytac o tych relacjach . Juz zapomnialem niestety

Maslanek: No ja też logikę w tamtym semestrze miałem, ale pojęcie przechodniości jeszcze znam Aczkolwiek nie mam pojęcia czasem co robisz, czytając Twoje posty Ale zdolność logicznego myślenia chyba zachowałem

5-latek: A moze to trzeba sobie wytlumaczyc tak : Jesli a nierownolegle do b i b nierownolegle do c to a nierownolegle do c dlatego ze czesc wspolna a I c jest zbiorem jednoelemntowym? Nie wiem czy dobrze mysle .

Maslanek: W definicji przechodniości masz, że dla dowolnych elementów a,b,c. Bierzemy więc takie, że a||c; a≠c. Jeżeli "~" jest relacją przecinania, to a~b znaczy tyle, że proste a i b się przecinają. b będzie prostą (choćby prostopadłą do a i c). Wtedy b przecina a i przecina c (relacja ~ jest symetryczna), tzn. a~b i b~c. Nieprawdą jest jednak, że a~c. (bo proste są równoległe). Wniosek: Relacja ~ nie jest przechodnia.

5-latek: Maslanek Probuje to dobrze zrozumiec gdyz potem bede musial zabrac sie za zadania z geometrii ze zbioru Trelinski Serafin . A tam juz nie ma zartow .

Maslanek: Nic mi to nie mówi Ale zapewne kiedyś tam dotrę Jeśli będę mógł pomóc, to spróbuję

5-latek: Nie widzialem twojego wpisu z 20:09. Wiec dziekuje za wyjasnienie . Juz jutro bede to analizowal .

5-latek: http://allegro.pl/trelinski-serafin-geometria-i4374208475.html to ten przykladowy zbior

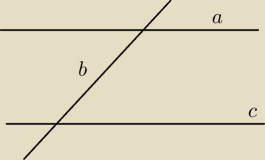
zawodus: a przecina b (a~b) b przecina c (b~c) ale a nie przecina c Czyli dokładnie jak opisał maślanek relacja nie jest przechodnia

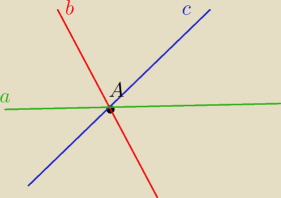
5-latek: Ale jak wezmiemy np pek prostych ? Wiem jestem upierdliwy ale chce to zrozumiec

Maslanek: Wtedy relacja mogłaby być przechodnia. Ale nie jest Nie jest, bo istnieje trójka prostych a,b,c dla których przechodniość nie działa. A skoro już takie znaleźliśmy znaczy, to tyle, że relacja nie jest przechodnia. Definicja przechodniości: ∀a,b,c (a~b ⋀ b~c ⇒ a~c). Zwróć uwagę na kwantyfikator: "Dla wszystkich". Jeżeli można podać kontrprzykład, to wiadomo co wnioskujemy

5-latek: Wiadomo czyli najpierw powtarzamy logike , relacje, a potem bierzemy sie za aksjomatyke

Maslanek: Nie wiem, co znaczy tu aksjomatyka Resztę słów rozumiem

Mila: Ładnie. Jak to dobrze, że zawodus i maslanek wyjaśnili. Nie lubię takich zadań. Po przeczytaniu treści staję się blondynką. I po co to robisz 5−latku?

5-latek: Dobry wieczor po raz drugi Milu jest to zadanie z ksiazki do geometrii dla klas 1 i2 liceum ogolnoksztalcacego i 1 2 3 technikum Krygowskiej Jet to zadanie nr 17 z tej ksiazki a wiec sa to poczatkowe wiadomosci o prostych przecinajacych sie i rownoleglych . Osobiscie tych zadan nie wymyslam ale przepisuje je z ksiazki Tam tez jest to wyjasnienie o stosunku rownoleglosci prostych ze jest zwrotny ,symetryczny i przechodni . Zaraz na poczatku ksiazki o odzworowaniu zbiorow jest relacja poprzedzania (antysymetria spojnosc przechodniosc . Wlasnie zeby to dobrze zrozumiec (a moze nie trzeba ) zamowilem sobie ksiazke Z. Opial. Zbiory formy zdaniowe relacje Ale tez chcialbym tez dopytac na forum