Ciągłość funkcji. Blue: Bok kwadratu ABCD ma długość 2√2. Wierzchołki K i L trójkąta równoramiennego AKL (gdzie |AK|=|AL|) należą do boków kwadratu. Przedstaw pole P trójkąta AKL jako funkcję jego wysokości x (gdzie x= |AE|). Określ dziedzinę funkcji P. Zbadaj ciągłość tej funkcji i naszkicuj jej wykres. Żeby nie było, że tylko skanuję, a nie chce mi się pisać, to przepisałam treść, jednak sądzę, iż bez rysunku tutaj się nie obejdzie , więc załączam też skan http://pl.tinypic.com/view.php?pic=eah8jb&s=8#.U63QsJrwGM_

Mila: Napisz Twoje propozycje.

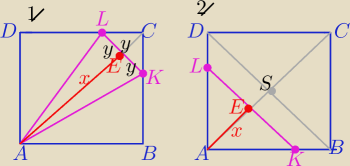
Eta: 1/ |AC|=4 |AE|=x , x>0 i y=4−x , x∊(0,4) PΔAKL= (4−x)*x ⇒P(x)= −x²+4x 2/ |AC|=|DB|=4 , |AE|=x z podobieństwa trójkątów ABD i AKL

	|KL|		x
		=		⇒ |KL|=......
	|DB|		|AS|

P= ........

Saizou : dalej sam

Piotr 10: sama

Saizou : a tak xd nie doczytałem końcówek ten niebieski

Blue: x= √y²−8y+16 I wtedy ta funkcja będzie wyglądać tak : f(y) = y*√y²−8y+16 I nie za bardzo wiem, skąd wiemy , że tam wszystkie te odcinki mają taką samą długość − y

zawodus: Ten mały odcięty trójkąt jest połową kwadratu dlatego tam wszędzie masz 'y' chodzi o przykład nr 1

Blue: ale nadal nie wiem jak to wyliczyć, jakoś to zadanie dla mnie jest dziwne..

zawodus: Pierwszą część ci przecież Eta policzyła pole To polecenie z ciągłością i wykresem to nie wiem po co

Blue: a dobra już widzę, bo Saizou mi to zagmatwał, a Eta przecież już to wyliczyła xD

Blue: Eta a mogłabyś jeszcze ten drugi trójkąt dokończyć i napisz mi proszę dlaczego w odpowiedziach mam, że P(x) = x² dla x ∊(0,2) i P(x) = 4x−x² dla x∊<2,4)?

zawodus: Te odpowiedzi dla którego podpunktu?

Blue: dla obydwu

zawodus: Tak w pierwszym powinno być P(x)=4x−x², x∊<2,4) Bo tylko od połowy przekątnej w ten sposób liczymy Drugie sama pomyśl

Blue: Boże jaka ja głupia, dobra już czaje to drugie, |KL| = 2x i potem pole = x² no tak. Mam już dość matmy, muszę sobie zrobić przerwę , bo nie myślę już