pole obszaru ograniczonego
Eliza: Oblicz pole obszaru ograniczonego wykresami funkcji y = 4x − x2 oraz y = x − 4
27 cze 15:16
zawodus: rysunek najpierw
27 cze 15:17
J: Znajdż odcięte punktów przecięcia , to będą granice całkowania.
27 cze 15:19
Eliza: 4x − x2 = x − 4
4x − x2 − x +4 = 0
− x2 + 3x +4 = 0
Δ = 32 − 4 * (−1) * 4
Δ = 25
√Δ = 5
x1 = −3−52*(−1) x1 = 4
x2 = −3+52*(−1) x2 = −1
27 cze 15:55
mika:
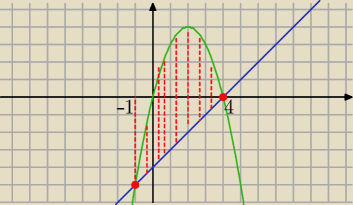
27 cze 16:00
Eliza: ∫4−1 (4x − x2 − (x−4))dx = ∫3−1 (−x2 + 3x +4)dx = (−12x + 341) = (−12 * 4 +3)
− (−12 * (−1) + 3) = 1 − 72 = [−212] = 2!2
27 cze 16:06
Eliza: Dziękuje za wykres
Czy rozwiązane jest dobrze?
27 cze 16:09
Mila:
Błędnie obliczona całka nieoznaczona.
| | 1 | | 3 | |
[− |
| x3+ |
| x2+4x]−14= licz teraz |
| | 3 | | 2 | |
27 cze 16:22
zawodus: Sama całka ok, a dalej to nie chce mi się sprawdzać
27 cze 16:23
J: | | 1 | |
Zacznijmy od tego,że źle policzyłaś całkę ... ∫ −x2 + 3x + 4 = − |
| x + 3 ? |
| | 2 | |
27 cze 16:24
J: No ... to już masz policzoną...
27 cze 16:25