,
Pi: Podstawą ostrosłupa ABCS jest trójkąt równoramienny ABC, w którym kąt ostry między ramionami AB
i Ac ma miarę . Sciana boczna BCS jest przystająca do trójkąta ABC i prostopadła do
płaszczyzny podstawy. Wykaż, że krawędź BS tworzy z krawędzią AB taki kąt, że cosβ =
sin2α2
25 cze 13:50
pigor: .., uzupełnij treść ...
... kąt ostry między ramionami AB i Ac ma miarę... jaką , α czy β

.
25 cze 14:01
Pi: kąt ostry między ramionami AB i Ac ma miarę α
25 cze 19:02
Mila:
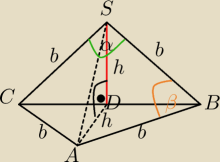
W ΔADS:
|AS|
2=h
2+h
2
|AS|
2=2h
2
WΔSDC:
WΔABS:
|AS|
2=b
2+b
2−2b
2 cos β
2h
2=2b
2*(1−cosβ) /:(2b
2)
===========
cnw
25 cze 21:28
pigor: ..., podstawą ostrosłupa ABCS jest trójkąt równoramienny ABC, w którym
kąt ostry między ramionami AB i AC ma miarę α. Ściana boczna BCS jest przystająca
do trójkąta ABC i prostopadła do płaszczyzny podstawy. Wykaż, że krawędź BS tworzy
z krawędzią AB taki kąt β, że
cosβ = sin2α.
−−−−−−−−−−−−−−−−−−−−−−−−
lub do swojej ...

szuflady schowam coś takiego: otóż z warunków zadania
|AB|=|AC|=|BS|=|CS|, |∡BAS|=|∡BSC|=α, |∡ABS|=β i niech
A' − rzut prostokątny A i S na BC (spodek wysokości),czyli |AA'|=|SA'|=H ⊥ BC,
a A'' − rzut prostokątny A' na AB, czyli A'A''⊥ AB, to ΔBA''A'∼ΔBA'A≡ΔBA'S (kkk)
trójkąty prostokątne o kątach |∡BSA'|=|∡BA'A''|=
12α, a wtedy
| | |BA'| | | |BA''| | |
z ΔBA'S: (*) |
| = sin12α i z ΔBA''A': (**) |
| =sin12α |
| | |BS| | | |BA'| | |
| | |BA''| | |
i z ΔBA''S (prostokątny, dlaczego  ) |
| =cosβ, stąd i mnożąc |
| | |BS| | |
| | |BA''| | |
stronami (*) i (**): |
| = sin212α = cosβ . ...c.n.w. ...  |
| | |BS| | |
26 cze 11:43
pigor: ..., kurde w przytoczonej "swojej" treści zadania sknociłem,
bo napisałem
cosβ= sin2α.,a przecież powinno być
cosβ= sin212α.,
juz poprawiam w ... szufladzie...

.
26 cze 11:49
 .
.
 W ΔADS:
|AS|2=h2+h2
|AS|2=2h2
WΔSDC:
W ΔADS:
|AS|2=h2+h2
|AS|2=2h2
WΔSDC:
 szuflady schowam coś takiego: otóż z warunków zadania
|AB|=|AC|=|BS|=|CS|, |∡BAS|=|∡BSC|=α, |∡ABS|=β i niech
A' − rzut prostokątny A i S na BC (spodek wysokości),czyli |AA'|=|SA'|=H ⊥ BC,
a A'' − rzut prostokątny A' na AB, czyli A'A''⊥ AB, to ΔBA''A'∼ΔBA'A≡ΔBA'S (kkk)
trójkąty prostokątne o kątach |∡BSA'|=|∡BA'A''|=12α, a wtedy
szuflady schowam coś takiego: otóż z warunków zadania
|AB|=|AC|=|BS|=|CS|, |∡BAS|=|∡BSC|=α, |∡ABS|=β i niech
A' − rzut prostokątny A i S na BC (spodek wysokości),czyli |AA'|=|SA'|=H ⊥ BC,
a A'' − rzut prostokątny A' na AB, czyli A'A''⊥ AB, to ΔBA''A'∼ΔBA'A≡ΔBA'S (kkk)
trójkąty prostokątne o kątach |∡BSA'|=|∡BA'A''|=12α, a wtedy
 )
) 
 .
.