Zamiana zmiennych w całce podwójnej. Czy mógłby ktoś obliczyć. Daniel: ∬_D (2y+x)dxdy, D={(x,y)∊R²:x²−1≤y≤2−2x²} oraz ∬_D √x²+y²dxdy, D: x²+y²≤1

Daniel: Pomoże ktoś? Bardzo mi zależy.

Godzio: Druga całka: x = rcos(a) y = rsin(a) x² + y² = r² ≤ 1 ⇒ r ∊ [0,1] ∫₀^2π∫₀¹r²dr (jeden promień z x² + y², drugi z jakobianu)

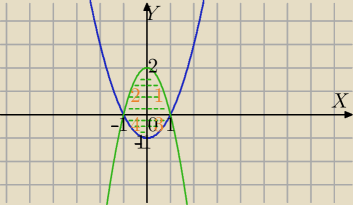
Mila: 1) Najpierw całkowanie względem zmiennej y, a następnie względem zmiennej x ( w granicach stałych) ₋₁∫¹[_x²−1∫^2−2x2(2y+x)dy] dx 2) Najpierw całkujemy względem x , potem względem y Ustalamy zmienne granice y≥x²−1 y=x²−1 x²=y+1 x=√y+1 (obszar (3) lub x=−√y+1 ( obszar (4) −1≤y≤0 y≤2−2x² x=√1−0,5y lub x=−√1−0.5y 0≤y≤2 Obszar (1 i 2) J₁=₀∫² [_{x=√1−0.5y}∫^{x=√1−0.5y}(2y+x)dx]dy= licz obszar (3i 4) J₂=₋₁∫⁰ [_−√y+1∫^√y+1(2y+x)dx]dy=.. dalej poradzisz sobie?

Daniel: Rozumiem, dziękuję bardzo za pomoc.

Mila: