Dlugość dwóch punktów wspolnych okręgów
Deyaas: Okręgi o równaniach (x−36)2+(y−15)2=1600 i x2+y2=625 mają dwa punkty wspólne A i B.
Uzasadnij, że |AB| = 48.
Prosiłbym aby ktoś podał mi sposób inny niż liczenie współrzędnych punktów A i B i ich długości
z równania.
24 cze 11:57
zawodus: Dlaczego? ta metoda jest wg mnie najkrótsza

24 cze 12:29
Bogdan:
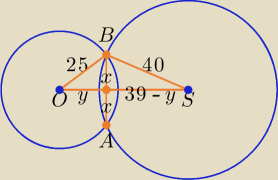
Można tak spróbować:
O(0, 0), S(36, 15), |OS| =
√362 + 152 = 39
x
2 + (39 − y)
2 = 1600
x
2 + y
2 = 625
(−) −−−−−−−−−−−−−−−−−−−
(39 − y)
2 − y
2 = 975 ⇒ (39 − y − y)(39 − y + y) = 975 ⇒ 39 − 2y = 25 ⇒ y = 7
|AB| = 2x = 2*
√252 − 72 = 2*24 = 48
24 cze 13:21
Bogdan:
| | 1 | |
albo w tym samym trójkącie OSB: połowa obwodu p = |
| 925 + 40 + 39) = 52 |
| | 2 | |
Pole trójkąta
P
OSB =
√52 * (52 − 25) * (52 − 40) * (52 − 39) =
√4*13 * 9*3 * 3*4 * 13 = 4*13*9
oraz
| | 1 | | 1 | | 4*13*9 | |
POSB = |
| *39*x ⇒ |
| *39*x = 4*13*9 ⇒ x = |
| = 24 |
| | 2 | | 2 | | | |
|AB| = 2x = 48
24 cze 13:39

 Można tak spróbować:
O(0, 0), S(36, 15), |OS| = √362 + 152 = 39
x2 + (39 − y)2 = 1600
x2 + y2 = 625
(−) −−−−−−−−−−−−−−−−−−−
(39 − y)2 − y2 = 975 ⇒ (39 − y − y)(39 − y + y) = 975 ⇒ 39 − 2y = 25 ⇒ y = 7
|AB| = 2x = 2*√252 − 72 = 2*24 = 48
Można tak spróbować:
O(0, 0), S(36, 15), |OS| = √362 + 152 = 39
x2 + (39 − y)2 = 1600
x2 + y2 = 625
(−) −−−−−−−−−−−−−−−−−−−
(39 − y)2 − y2 = 975 ⇒ (39 − y − y)(39 − y + y) = 975 ⇒ 39 − 2y = 25 ⇒ y = 7
|AB| = 2x = 2*√252 − 72 = 2*24 = 48