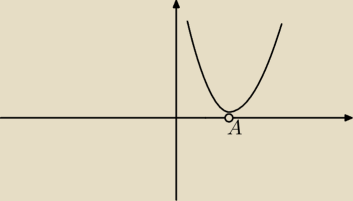
nierównosc wykładnicza tyu: proszę o podpowiedź mam nierówność 3^2x+2−2*3^x+2 − 27 <0 podstawiam t=3^x i wychodzi mi t²*9−2*t*9−27<0 9t²−18t−27<0 t₁=−1 t₂=3 t₁=−1 nie doprowadzę do postaci potęgi o podstawie 3, więc pozostaje mi t₂=3 więc x=1 i ramiona do góry paraboli do góry idą, zatem wykres nie ma miejsc wspólnych z osią OX, a w odpowiedziach jest napisane x∊(−∞;1) rys. A=−1

Piotr 10: Troszkę źle koncowke zaczynasz, moja sugestia: t₁= − 1 v t₂ = 3 ( to sa nasze m_o) Teraz rysujemy szkic paraboli: dla funkcji 9t² − 18t − 27 < 0 A więc t∊( − 1 ; 3 ) Czyli: − 1 < t < 3 t=3^x − 1 < 3^x < 3 Tutaj obowiazuje nas cześć wspolna czyli spojnik 'i' 1⁰ −1 < 3^x i 2⁰ 3^x < 3 1⁰ Jest spelnione dla kazdego x∊R 2⁰ 3^x < 3¹ Jest to funkcja rosnąca, więc nie zmieniamy znaku x < 1 1⁰ ⋀ 2⁰ ⇔ x∊ ( − ∞ ; 1)

tyu: dzięki za odpowiedź. Już czytam co napisałeś

tyu: rozumiem. 1⁰ i 2⁰ to jest odpowiednio przypadek nr 1 i nr 2, a nie 1⁰=1 i 2⁰=1, bo to jest trochę mylące. Czyli tutaj istotne jest, że −1 < 3^x jest spełnione dla każde x∊R (wykres czerwony) 3^x < 3¹ i x < 1 (wykres czarny) i teraz zaznaczam część wspólną (zielony) rys. A=1

Piotr 10: Uwaga: 1⁰ i 2⁰ to nie jest PRZYPADEK. Przypadek tyczy się sumy, a my tutaj robimy część wspólną. Reszta ok dobrze myślisz. 1⁰ i 2⁰ to po prostu moje oznaczenia. Mnie tak w szkole uczono

tyu: Dziękuję za pomoc.

Piotr 10: Nie ma za co