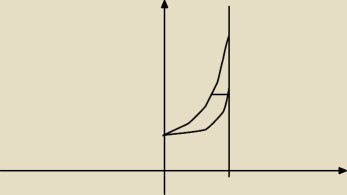
calka student: zamień kolejność całkowania w całce, proszę o pomoc _{2 3}x ∫dx ∫f(x,y)dy ⁰ 2^x (1 calka od 0 do 2) (2 calka od 2^x do 3^x) D={0≤x≤2, 2^x≤y≤3^x D₁={ ≤x≤ , 1≤y≤4 D₂={ ≤x≤ , 4≤y≤9 Podzieliłem na 2 obszary, ale nie wiem jak ogranicza x, jak zamienić y=2^x, żeby wyliczyć x?

student:

student: D₁ na dole, D₂ górna cześć

student: up.

Mila:

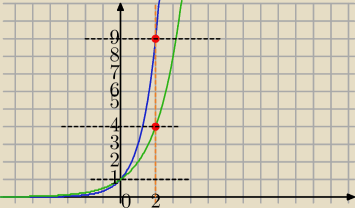
	ln(y)
y=2x stąd ln(y)=x*ln(2), x=
	ln(2)

2²=4

	ln(y)
y=3x stąd ln(y)=x*ln(3), x=
	ln(3)

3²=9

	ln(y)		ln(y)
1≤y≤4 w jednej całce ,		≤x≤
	ln(3)		ln(2)

	ln(y)
4≤y≤9 w drugiej całce,		≤x≤2
	ln(3)

student: super możesz podać jeszcze wzór na ln, który był potrzebny, a ja go nie kojarzę

student: .

student: możesz napisać ten wzór z którego wyznaczyłeś/łaś x ?

student: dobra chyba znalazłem i wyszło proszę o potwierdzenie: 2^x=y /ln ln2^x=lny xln2=lny /:ln2

	lny
x=
	ln2

Mila: y=2^x logarytmujemy obustronnie ln(y)=ln(2^x)⇔ ln(y)=x ln(2) [ln(a^b)=b* ln(a) ]

student: jeszcze pytanie: lne⁽|x|) to jest x lub −x(bo moduł) ?

student: lne^|x|

student: a mam do obliczenia y=e^|x| lny = lne^|x| lny= |x|lne

	lny
|x|=
	lne

|x|=lny lny=x lub −x, bo chyba tak nie wolno robić...

student: chociaż chyba można tak zrobić

student: jeszcze jak możesz odp to bd naprawdę usatysfakcjonowany

Mila: ln(e^|x|)=|x| Jeśli nie masz ograniczeń w treści ( co do znaku x) zadania to korzystasz z definicji wartości bezwzględnej.

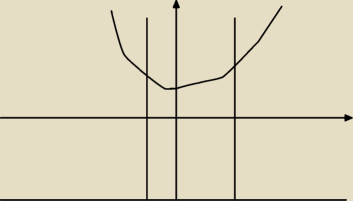
student: podobne zadanie do wcześniejszego: calka od −1 do 2 dx calka od −−3 do e^|x| tutaj trzeba podzielić na 3 obszary?

student: D₁={−3≤x≤−lny, −1≤y≤0 D₂={−3≤x≤lny, 0≤y≤2 jednak na 2 dobrze?

student:

Mila: 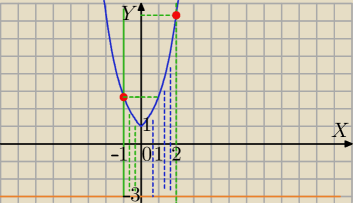y=e^|x| e^|−1|=e e² Chcesz mieć obszary normalne względem OX, czy OY ( tzn. zmienić granice całkowania?)

Mila: Będę za godzinę.

student: zmienic kolejnosc calkowania w całce: ∫dx ∫f(x,y)dy 1 calka od −1 do 2 2 calka od −3 do e^|x|

student: okej na pewno odczytam

Mila: Jakie masz propozycje?

student: takie jak wyżej napisałem, ale nie wiem czy to jest poprawnie

student: D₁={−3≤x≤−lny, −1≤y≤0 D₂={−3≤x≤lny, 0≤y≤2

student: dobra jeszcze raz zrobilem i mi wyszlo: D₁={ −1≤x≤−ln(y), −3≤y≤1 D₂={ 0≤x≤ln(y), −3≤y≤1

Mila: Np. 3 obszary: 1) 1≤y≤e −1≤x≤−ln(y) 2)1≤y≤e² ln(y)≤x≤2 3) prostokąt, to sam ustal

student: y=e^|x| /ln lny=lne^|x| |x|={ x gdy x≥o, −x gdy x<0 lny=x −lny=x jednak wybieram 1 opcje: D₁={−3≤x≤−lny, −1≤y≤0 D₂={−3≤x≤lny, 0≤y≤2 dobrze?

Mila: Oblicz całkę na dwa sposoby, a nawet 3, bo taka podwójna całka to pole tego obszaru.

student: 1≤y≤e y=1 y=e nie pasuje bo mamy max do 2

student: a jednak pasuje

Mila: No, nie , miałeś podane: −3≤y≤e^|X| −1≤x≤2 Poprowadź prostą y=1 i odetnij prostokąt, u góry masz dwa obszary. Czerwone kropki to y=e^|−1|=e i y=e^|2|=e² Czy narysować jeszcze raz? Masz odpowiedź do zadania?

student: już rozumiem całe zadanie

	1
e|−1|=e cały czas wydawało mi się ze to jest		ślepy bylem modułu nie widziałem
	e

już widzę 3 obszary: D₁= {−1≤x≤−lny, 1≤y≤e D₂={ 0≤x≤2, 1≤y≤e² D₃={ −3≤x≤1, −1≤y≤2 odpowiedzi brak, bo to zadanie z kolokwium bardzo dziękuję za pomoc

student: D2={ lny≤x≤2, 1≤y≤e2

student: D3={ −1≤x≤2, −3≤y≤1 ah te literówki

Mila: Trzeci popraw. I licz całkę.

Mila: Teraz dobrze. Jeszcze jestem, to podaj wynik. Ja też miałam rozbieżności w rachunkach , bo w części zadania dałam krzywą y=2^|x|.

student: nie trzeba liczyć całki, trzeba tylko zamienić kolejność całkowania i narysować obszar, ale to już udało się zrobić więc koniec jeszcze raz dziękuję

Mila: No to miło.