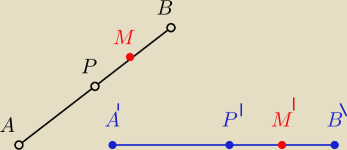
obraz odcinka w izometrii 5-latek: Chyba juz troche za pozno na nauke . Juz nie bardzo rozumie pewnych rzeczy . Otoz robie dowod na to ze obrazem odcinka AB w izometrii jest odcinek A'B' a obrazem jego koncow AB jego konce A'B' Robie to z ksiazka i pierwsza czec dowodu iz dowolny punkt odcinka AB przeksztalca sie na punkt odcinka A'B' rozumien Tutaj wykazalismy z epunkty sa wspoliniowe wiec punkt P' lezy pomiedzy A'B' W drugiej czesci dowodu mamy wylkazac ze kazdy punkt odcinka A'B' przeksztalca sie na punkt odcinka AB Teraz jest tak : Niech M' bedzie dowolnym punktem odcinka A'B' a M jego obrazem w przeksztalceniu T⁻¹ odwrotnym wzgledem T (gdzie T jest jakimkolwiek przeksztalceniem izometrycznym Nie ma tego zapisanego w ksiazce ale moge zapisac to tak T⁻¹(M')=M i powinno to byc prawidlowe wedlug mnie jezeli M'=A' to M=A gdyz w przeksztalceniu T⁻¹ punkt A' przeksztalca sie na punkt A czyli A jest obrazem punktu A" w przeksztalceniu T⁻¹ (zapiszse to po swojemu T⁻¹(A')=A Podobnie jezeli M'=B' to M=B bo w przeksztalceniu T⁻¹ punkt B" przeksztalca sie na B czyli T⁻¹(B')=B Teraz jesli punkt M' lezy miedzy punktami A'B' to A'M'+M'B'=A'B' Poniewaz przeksztalcenie T⁻¹ jet izometryczne (dodaje od siebie bo do kazdej izometrii mozna wskazac przeksztalcenie odwortne ktore tez jest izmometria) wiec A'M'+AM i M'B'= MB i wlasnie tego zapisu nie rozumiem wedlug mnie jest to blad bo powinno byc chyba A'M'=AM i M'B'=MB . czy moze ktos mi to wytlumaczyc bo przeciez nie chodzi o to ze A'M'+AM=A'B'bo to nie jest prawda

Mila: Masz rację znak ( +) się przyplatał zamiast (=)

5-latek: Milu serdecznie dziekuje dalej autor wykazuje ze gdy (M' lezy miedzy A' B' ) to punkt M jest punktem wewnetrzym odcika AB Wykazuje to poprzez dowod nie wprost (czyli pumt M nie nalezy do odcinka AB wiec ten punkt M 1> MUsialby by lezec poza prosta AB 2. Na jednym z przedluzen odcinka AB poza punkt A lub punkt B 3. Trzecia mozliwosc M=A odpada poniewaz T(A)=A' nie rowna sie M to samo nie moze byc M=B Pytanie dlaczego trzecia mozliwosc odpada ? . Przeciez na poczatku napisalismy ze M=A i M=B czy tu moze chodzi o to ze punkt wewnetrzny odcinka to kazdy punkt pomiedzy jego koncami czy moze o co innego ?

5-latek: Albo to bedzie mialo zwiazek z przeksztalceniami (ale jeszce tego nie lapie

Toskan: Kwestia tego co autor rozumie przez leżenie punktu pomiędzy dwoma innymi. Jeżeli będziemy tłumaczyć dosłownie to oczywiście trzecia możliwość jak najbardziej istnieje bo z góry mamy założone, że M' leży pomiędzy A' i B'. Rozważmy przedziały x∊(5, 7) y∊<10, 15> Tylko w pierwszym przypadku powiemy, że x leży pomiędzy 5 a 7. W drugim przypadku czy możemy powiedzieć, że y leży pomiędzy 10 a 15? Ja bym tak nie powiedział.

5-latek: Witam. dziekuje za zainteresowanie

5-latek: A moze tu chodzi o to ze jesli jet M=A a my robiny dowod nie w wprost to wtedy M≠A?

5-latek: Moze to troche wyglada glupio . Bo tak jakbym prowadzil dialog sam ze soba, ale jest to dla mnie wazne . Wlasnie ksiazka ma ta przewage ze mozna bez przerwy wracac do niezrozumialego tekstu . Juz wiem dlaczego to trzecia mozliwosc odpada

Maslanek: Jeżeli M=A, to przekształcenie nie jest izometrią, gdyż izometria jest różnowartościowa

Maslanek: Tzn., jesli A'≠M' i T(A')=A, to nie może być T(M')=A.

Maslanek: Fajnie by było jakbyś przybliżył dowód dwóch pierwszych punktów Domyślam się, że w 2) pokazujemy odległość punktów. Co z 1)? (nierówność trójkąta)?

5-latek: Dziekuje za odpowiedz Jest tak jak napisales . W pierszym korzystamy z nierownoscici trojkata bo bedzie AM+MB>AB co wobec rownosci AB=A'B' i tych wyzej jest niemozliwe W drugim korzystamy z odleglosci punktow Jesli przyjmiemy ze punkt M lezy poza punkt B to AB+BM+AM co wobec poprzednich rownosci jest niemozliwe