Ciekawostka Trudna
Seta222: Witam trafiło mi sie na kolokwium zaliczeniowym pewne zadnie co nie mogłem zrozumieć i szukam
pomocy jak je rozwiązać

POle miedzy wykresem funkcji f(x)=sinx a osią OX dla x∊{−π,π}
Prosze o pomoc

20 cze 20:01
AS:
P1 = ∫[0,π]sin(x)dx
P2 = ∫[−π,0]sin(x)dx
P = P1 + |P2|
20 cze 20:04
Seta222: No ok , ale pole wychodzi 0

A ja mam inne odpowiedzi

20 cze 20:06
sushi_ gg6397228:
jak pole wychodzi 0?
20 cze 20:12
Seta222: No normalnie wychodzi 0

20 cze 20:15
xxxx:
Bzdura jakie zero

!
20 cze 20:18
Seta222: A ile ?
20 cze 20:19
sushi_ gg6397228:
policz to
20 cze 20:19
xxxx:
4
20 cze 20:20
Seta222: No ale jak

∫(0−sinx)dx{0,−π} z tego wychodzi {−cosx} {0,−π} i z tego −cos0+cos−π = 0 Robię błąd

20 cze 20:25
sushi_ gg6397228:
narysuj wykres sinusa i myśl
20 cze 20:27
Seta222: Ale na co mi wykres sinusa jak mam całkę z cosinusa ?
20 cze 20:29
sushi_ gg6397228:
bo liczysz pole pod wykresem sinusa
i pole jest dodatnie
to widać, że jak się włączy myślenie, to trzeba podzielić obszar całkowania na pół
20 cze 20:32
Seta222: Z całym szacunkiem nie rozumię

20 cze 20:33
sushi_ gg6397228:
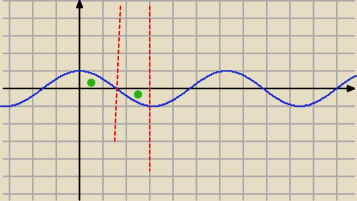
jak mi teraz powiesz ze pole z kropkami zielonymi jest równe zero, to,,,,,,,
20 cze 20:35
Seta222: Nie obraź się kolego drogii ale czemu teraz odczytujemy pole z cosinusoidy tylko z prawej
strony ?

Chyba mam jakis słabszy dzień

20 cze 20:40
sushi_ gg6397228:
masz pole P1 do policzenia
pole P2 będzie takie samo
20 cze 20:42
Seta222: ∫(0−sinx)dx{0,−π} z tego wychodzi {−cosx} {0,−π} i z tego −cos0+cos−π = 0 Robię błąd To gdzie
w moim liczeniu jest błąd

20 cze 20:44
sushi_ gg6397228:
szkoda zdrowia
20 cze 20:45
Seta222: Lub nie potrafisz dość wystarczająco wytłumaczyć


20 cze 20:48
Mila:
Teoria :
Jeśli w przedziale <a,b> jest
f(x)≥0 to pole obszaru ograniczonego krzywą i osią Ox,
prostymi x=a i x=b równa się całce:
a∫
b f(x) dx
W twoim przypadku:
P
1={0∫
π(sin(x) dx=[−cos(x)]
0π=−cosπ+cos0=−(−1)+1=2
Jeśli w przedziale <a,b> jest
f(x)<0 to pole obszaru ograniczonego krzywą i osią Ox,
prostymi x=a i x=b równa się całce:
−a∫
b f(x) dx
P
2=
−−π∫
0(sin(x) dx=[cos(x)]
0π=cos0−cos(−π)=1−(−1)=2
P=2+2=4
20 cze 21:05
Godzio:
A ogólniej, pole między dwoma funkcjami f i g to
∫
ab(f − g)dx gdzie funkcja f jest "nad" funkcją g w tym przedziale,
W tym przypadku, jedna funkcja to f = 0 i mamy:
∫
ab(0 − g)dx = − ∫
abgdx

20 cze 21:09
setardg: Dziękuję Państwu

20 cze 21:25
Mila:

20 cze 21:26
 POle miedzy wykresem funkcji f(x)=sinx a osią OX dla x∊{−π,π}
Prosze o pomoc
POle miedzy wykresem funkcji f(x)=sinx a osią OX dla x∊{−π,π}
Prosze o pomoc 
 A ja mam inne odpowiedzi
A ja mam inne odpowiedzi 

 !
!
 ∫(0−sinx)dx{0,−π} z tego wychodzi {−cosx} {0,−π} i z tego −cos0+cos−π = 0 Robię błąd
∫(0−sinx)dx{0,−π} z tego wychodzi {−cosx} {0,−π} i z tego −cos0+cos−π = 0 Robię błąd 

 jak mi teraz powiesz ze pole z kropkami zielonymi jest równe zero, to,,,,,,,
jak mi teraz powiesz ze pole z kropkami zielonymi jest równe zero, to,,,,,,,
 Chyba mam jakis słabszy dzień
Chyba mam jakis słabszy dzień 



 Teoria :
Jeśli w przedziale <a,b> jest f(x)≥0 to pole obszaru ograniczonego krzywą i osią Ox,
prostymi x=a i x=b równa się całce:
a∫b f(x) dx
W twoim przypadku:
P1={0∫π(sin(x) dx=[−cos(x)]0π=−cosπ+cos0=−(−1)+1=2
Jeśli w przedziale <a,b> jest f(x)<0 to pole obszaru ograniczonego krzywą i osią Ox,
prostymi x=a i x=b równa się całce:
−a∫b f(x) dx
P2=−−π∫0(sin(x) dx=[cos(x)]0π=cos0−cos(−π)=1−(−1)=2
P=2+2=4
Teoria :
Jeśli w przedziale <a,b> jest f(x)≥0 to pole obszaru ograniczonego krzywą i osią Ox,
prostymi x=a i x=b równa się całce:
a∫b f(x) dx
W twoim przypadku:
P1={0∫π(sin(x) dx=[−cos(x)]0π=−cosπ+cos0=−(−1)+1=2
Jeśli w przedziale <a,b> jest f(x)<0 to pole obszaru ograniczonego krzywą i osią Ox,
prostymi x=a i x=b równa się całce:
−a∫b f(x) dx
P2=−−π∫0(sin(x) dx=[cos(x)]0π=cos0−cos(−π)=1−(−1)=2
P=2+2=4


