Wyznacz wszystkie wartości parametru a today: Wyznacz wszystkie wartości parametru a dla których równanie: |x+5| = a³ + 2a² − a − 2 ma rozwiązanie.

alfa: |x+5| = a³ + 2a² − a − 2 Równanie to będzie miało rozwiązania, gdy a³ + 2a² − a − 2 ≥ 0, gdyż wartość bezwzględna musi być nie mniejsza od zera. Równanie to będzie miało 1 rozwiązanie gdy a³ + 2a² − a − 2 = 0, czyli dla a = −2 lub a = −1 lub a = 1. Równanie to będzie miało dwa rozwiązania dla (−2;−1) u (1; +∞).

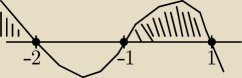
today: Dzięki za rozwiązanie, tylko nie rozumiem tego przedziału dla których równanie będzie miało 2 rozwiązania bo mi wyszło takie coś: a³>0 więc od góry zacząłem rysować, a rownanie ≥ 0 więc obszar nad osią Ox, czyli rozwiązania to a∊(−∞,−2> u <−1,1> dobrze myślę?

alfa: Źle narysowałeś wykres a³ + 2a² − a − 2 ≥ 0. Wykres będzie leżał nad osią OX dla (−2;−1) u (1; +∞) i wtedy będą dwa rozwiązania. Dla miejsc zerowych wielomianu a³ + 2a² − a − 2 równanie wyjściowe będzie miało jedno rozwiązanie.

today: a mógłbyś naszkicować jak powinien wyglądać ten wykres? bo nie kapuje

alfa: W tym linku jest poprawny wykres: http://img691.imageshack.us/img691/2403/wykresg.jpg

today: wiem już gdzie popełniłem błąd, rysowałem wykres od lewej a rysuje sie od prawej... Dzięki za pomoc