ff:
Nie rozwiązuj tego ze względu na x,y a raczej szukając: x
2+y
2 − dla podstawienia walcowego.
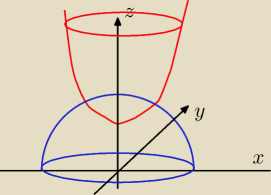
Narysuj to sobie, masz 2 powierzchnie: paraboloidę i połowę sfery
(właściwie do znalezienia wysokości przecięcia wystarczy przekrój w xz (podstawienie y=0)−
obydwie powierzchnie są obracane wokół 0z)
w przekrojach paraboloidy płaszczyznami równoległymi do xy masz okręgi o promieniach
(r
2=x
2+y
2), r =
√z−1 bo z = x
2 + y
2 + 1
dla sfery promienie to:
√5−z2 (z równania sfery: x
2+y
2+z
2=5 )
ich przecięcie (okręgi powstałe przy przecinaniu płaszczyznami równoległymi do 0xy będą miały
równe promienie) jest na wysokości z (
√5 ≥ z ≥0):
√5−z2 =
√z−1
5−z
2=z−1
z
2+z−6=0
z = 2
po zamianie na współrzędne walcowe (r,α,z) masz dla częsci sfery: z ∊ (2,
√5 ) , 0 ≤ r ≤
√5−z2
a dla części paraboloidy: z ∊ (1,2), r ≤
√z−1
 Nie rozwiązuj tego ze względu na x,y a raczej szukając: x2+y2 − dla podstawienia walcowego.
Narysuj to sobie, masz 2 powierzchnie: paraboloidę i połowę sfery
(właściwie do znalezienia wysokości przecięcia wystarczy przekrój w xz (podstawienie y=0)−
obydwie powierzchnie są obracane wokół 0z)
w przekrojach paraboloidy płaszczyznami równoległymi do xy masz okręgi o promieniach
(r2=x2+y2), r = √z−1 bo z = x2 + y2 + 1
dla sfery promienie to: √5−z2 (z równania sfery: x2+y2+z2=5 )
ich przecięcie (okręgi powstałe przy przecinaniu płaszczyznami równoległymi do 0xy będą miały
równe promienie) jest na wysokości z (√5 ≥ z ≥0):
√5−z2 = √z−1
5−z2=z−1
z2+z−6=0
z = 2
po zamianie na współrzędne walcowe (r,α,z) masz dla częsci sfery: z ∊ (2, √5 ) , 0 ≤ r ≤
√5−z2
a dla części paraboloidy: z ∊ (1,2), r ≤ √z−1
Nie rozwiązuj tego ze względu na x,y a raczej szukając: x2+y2 − dla podstawienia walcowego.
Narysuj to sobie, masz 2 powierzchnie: paraboloidę i połowę sfery
(właściwie do znalezienia wysokości przecięcia wystarczy przekrój w xz (podstawienie y=0)−
obydwie powierzchnie są obracane wokół 0z)
w przekrojach paraboloidy płaszczyznami równoległymi do xy masz okręgi o promieniach
(r2=x2+y2), r = √z−1 bo z = x2 + y2 + 1
dla sfery promienie to: √5−z2 (z równania sfery: x2+y2+z2=5 )
ich przecięcie (okręgi powstałe przy przecinaniu płaszczyznami równoległymi do 0xy będą miały
równe promienie) jest na wysokości z (√5 ≥ z ≥0):
√5−z2 = √z−1
5−z2=z−1
z2+z−6=0
z = 2
po zamianie na współrzędne walcowe (r,α,z) masz dla częsci sfery: z ∊ (2, √5 ) , 0 ≤ r ≤
√5−z2
a dla części paraboloidy: z ∊ (1,2), r ≤ √z−1