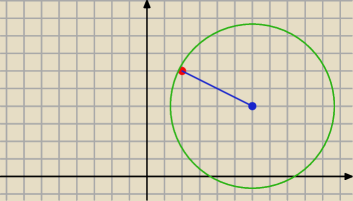
A#7 Lukas: Podane jest równanie okręgu x²+y−12x− 8y + 32 = 0 w okrąg ten wpisano trójkąt równoboczny ABC w którym A = (2;6 ) . Oblicz współrzędne pozostałych wierzchołków trójkąta. (x−6)²+(y−4)²=20 S=(6,4) r=2√5 a=2√15 i teraz chciałem zrobić z długości odcinka |AB|=2√15 Ale nie wiem jak to zapisać nie chcę robić tego zadanie wektorami tylko skończyć swoim sposobem

razor: 1) Oblicz odległość środka okręgu od punktu A 2) Wylicz długość boku trójkąta równobocznego 3) Stwórz równanie nowego okręgu o środku w punkcie A i długości promienia równej długości boku trójkąta 4) Nowy okrąg będzie przecinać stary okrąg w dwóch punktach które będą wierzchołkami trójkąta

Lukas: już wyznaczyłem długość boku, chcę dokończyć jednak swój pomysł.

razor: a jaki ten pomysł?

Mila: 1) Napisz równanie okręgu o środku A(2,6) i promieniu R=2√15 Znajdujesz punkty B i C jako punkty przecięcia z okręgiem (x−6)²+(y−4)²=20

Lukas: skorzystać ze wzoru na długość odcinka, napisałem wyżej przecież |AB|=2√15 tylko nie wiem jak zapisać to ?

Lukas: zrobię tamtym sposobem ale najpierw chcę dokończyć swoją myśl.

Lukas: np jak punkt nalezy do prostej y=x−4 (x−2)²+(x−4−6)²=60 ale jak to zapisać w przypadku okręgu ?

Mila: To właśnie podałam Ci sposób ze wzoru na długość odcinka do kwadratu , tak samo razor.

Lukas: Nie? Wy każecie tworzyć nowy okrąg, mi chodzi o coś innego..

razor: a co opisuje równanie okręgu? przecież to nic innego jak wszystkie punkty w określonej długości od środka

Lukas: ale to nie jest tak samo jak z punktem który leży na prostej, dobra odpuszczam to zadanie na razie.

Mila: Długość odcinka AB |AB|=2√15 B=(x,y) √(x−2)²+(y−6)²=2√15 masz długość AB, podnoszę obustronnie do kwadratu (x−2)²+(y−6)²=4*15 i to już jest równanie okręgu, Ponieważ B(x,y) leży na okręgu (x−6)²+(y−4)²=20, to musisz rozwiązać układ równań. Jeśli wiesz na jakiej prostej leżą A i B , to można inaczej.

Lukas: no własnie ja podałem przykład jak punkt leży na prostej..

Lukas: a po dwa czemu mam niby tworzyć nowe równanie okręgu ?

zawodus: Nie rozumiesz zatem w ogóle tego zadania.

Lukas: Rozumiem zadanie.

Mila: To w czym problem, umiesz cyrklem i linijką wykreślić, gdybyś znał długość boku?

Lukas: W okrąg wpisujemy trójkąt równoboczny..

5-latek:

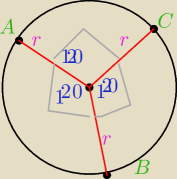
Mila: Właśnie, wbijasz cyrkiel w punkt A i kreślisz okrąg o promieniu a=2√15 i otrzymujesz punkty przecięcia z zielonym okręgiem (21:38). To przetlumacz teraz na czynności rachunkowe.

Mila: Pomysł pięciolatka ładny do konstrukcji, ale jak to przetłumaczyc na rachunki geometrii analitycznej?

Lukas: To wychodzi, że nie znam konstrukcji, ale czemu mając punkt należacy do prostej y=x+3 (x−3)+(x+3−4)=20 jakoś przykładowo podałem a dla okręgu tak nie można zrobić ?

Mila: Nie rozumiem zapisu z 21:45. Co tam zrobiłeś? Dlaczego nie odpowiesz mi na pytanie z 21:42?

Lukas: Nie wiem co mam robić mam tylko punkt.

Mila: Wbijasz cyrkiel w punkt A(2,6), czyli to jest środek okręgu kreślisz okrąg o promieniu równym 2√15 , czyli masz r=2√15 i srodek okręgu, to mozesz napisać rownanie tego okręgu: (x−2)²+(y−6)²=(2√15)² Następnie widzisz punkty przecięcia ,ale trzeba obliczyc wsp. , szukasz teraz punktów przecięcia z okręgiem zielonym, znasz równanie. W takim razie rozwiąż układ równań i otrzymasz wsp. punktów B i C.

Lukas: Dziękuję, spróbuje jakoś zrozumieć. Choć zawsze podobne zadania robiłem inaczej.

Mila: Mozesz zrobić swoim sposobem i porównamy wyniki.

Lukas: Właśnie nie mogę zrobić moim sposobem bo nawet nie wiem jak to zapisać.

Mila: No to chyba rozumiesz co napisałam 22:02, wykonaj.

Lukas: x²−12x+y²−8y=−32 x²+4x+y²−12y=20

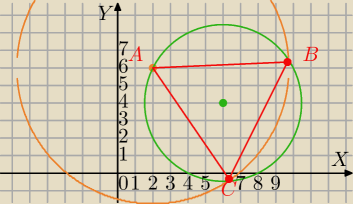
Mila: x²−12x+y²−8y=−32 x²−4x+y²−12y=20 odejmuje stronami −12x+4x −8y+12y=−32−20 −8x+4y=−52 4y=8x−52 y=2x−13 podstawiam do równania(x−6)²+(y−4)²=20 (x−6)²+(2x−13−4)²=20 x²−12x+36+4x²−68x+289−20=0 5x²−80x+305=0 /:5 x²−16x+61=0 Δ=256−244=12 √12=2√3

	16−2√3
x=		=8−√3 lub x=8+√3
	2

y=16−2√3−13=3−2√3 lub y=16+2√3−13=3+2√3 Zobacz, czy zgadza sie z odpowiedzią.

Lukas: Dziękuję, ale i tak jutro będę miał kilka pytań.

Mila: