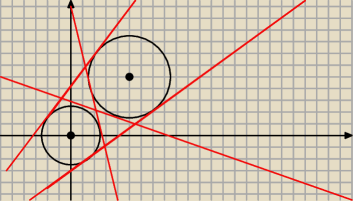
Wyznacz równania wspólnych stycznych do okręgów. Radek: Witam Wyznacz równania wspólnych stycznych do okręgów. Mam równania dwóch okręgów i mam napisać równania wspólnych stycznych ma ktoś pomysł jak to można rozwiązać ?

Lukas: Takich stycznych będzie n podaj treść zadani i dane !

Radek: x²+y²=5 oraz (x−5)²+(y−5)²=20

Radek: to są równania okręgu a treść jak wyżej

Radek: ma ktoś pomysł ?

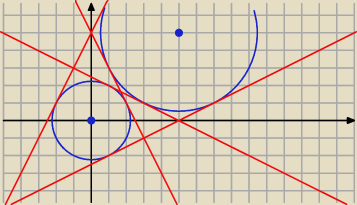
Bogdan: Styczna y = ax + b x² + y² = 5 i y = ax + b ⇒ x² + (ax + b)² = 5, stąd obliczamy Δ₁ oraz (x − 5)² + (y − 5)² = 20 i y = ax + b ⇒ (x − 5)² + (ax + b − 5)² = 20, stąd obliczamy Δ₂ Teraz trzeba rozwiązać układ równań z niewiadomymi a, b: Δ₁ = 0 i Δ₂ = 0 Otrzymamy 4 rozwiązania:

	1		5		1		5
1) a =		i b = −		⇒ y =		x −
	2		2		2		2

	1		5		1		5
2) a = −		i b =		⇒ y = −		x +
	2		2		2		2

3) a = 2 i b = 5 ⇒ y = 2x + 5 4) a = −2 i b = 5 ⇒ y = −2x + 5

Radek: x²+(a x+b)² = 5 a² x²+2 a b x+b²+x²−5 = 0 I jak z tego obliczyć deltę ?

razor: nie tak się podnosi do kwadratu x² + (ax+b)² = 5 (x−5)² + (ax+b−5)² = 20 x² + a²x² + 2abx + b² − 5 =0 x² − 10x + 25 + a²x² + b² + 25 + 2abx − 10b − 10ax − 20 = 0 (a²+1)x² + 2abx + b²−5 = 0 (a²+1)x² + (2ab−10a−10)x + b²−10b+30 = 0 Δ₁ = (2ab)² − 4(a²+1)(b²−5) = 0 Δ₂ = (2ab−10a−10)² − 4(a²+1)(b²−10b+30) = 0 taki przyjemny układ równań do obliczenia

Mila: Z odległości środka okręgu od prostej stycznej jest mniej rachunków. x²+y²=5 O=(0,0) , r=√5 (x−5)²+(y−5)²=20 , S=(5,5), R=2√5 1) odległość stycznej od punktu (0,0) s: styczna − y=ax+b⇔ax−y+b=0

|a*0−1*0+b|
	=√5⇔
√a2+1

|b|=√5*√a²+1 /² (*) b²=5*(a²+1) =========== 2) odległość stycznej od punktu (5,5)

|a*5−1*5+b|
	=2√5⇔|5a−5+b|=2√5*(√a2+1 /2
√a2+1

|5a+b−5|²=4*5(a²+1} korzystam z (*) i podstawiam |5a+b−5|²=4b²⇔ 5a+b−5=2b lub 5a+b−5=−2b

	5		5a
b=5a−5 lub −3b=5a−5⇔b=		−
	3		3

	5		5a
b=5a−5 lub b=		−
	3		3

============================= Wracamy do równania : b²=5*(a²+1) dla b=5a−5 mamy : (5a−5)²=5a²+5

	1
a1=		lub a2=2
	2

	5
b1=−		lub b2=5
	2

styczne (zewnętrzne)

	1		5
y=		x−		lub y=2x+5
	2		2

	5		5a
dla b=		−		mamy:
	3		3

	5		5a
(		−		)2=5*(a2+1)
	3		3

	5
(		)2*(1−a)2=5a2+5
	3

25
	*(1−2a+a2)=5a2+5 /*9
9

25−50a+25a²=45a²+45

	1
a=−2 lub a=−
	2

	5		10		5		5		5
b=		+		=5 lub b=		+		=
	3		3		3		6		2

Styczne ( wewnętrzne )

	1		5
y=−2x+5 lub y=−		x+
	2		2

==========================

Jacek: A można by takie zadanie na maturze rozwiązać bardziej geometrycznym sposobem i dostać komplet punktów?

123: W podobnym zadaniu mam problem, napiszę do do postu Mili 18:39 Zastosowałem najpierw równanie odległość S₁ od stycznej = odl S₂ od stycznej i po rozpisaniu na dwa przypadki z wartości bezwzględnej mam problem dwa równania stycznych wychodzą mi poprawnie lecz w tym przypadku współczynnik b się skraca i następnie korzystam z z odległość S₁ od stycznej = promieniowi dokładna liczba Lecz dla drugiego przypadku z wartości bezwzględnej jak wiadomo "b" się nie kasuje i potem po wyznaczeniu np a zależnego od b z tego równania i po wstawieniu podobnie do równania odl S₂ od stycznej = r wychodzi tylko jedna styczną i to błędna

123: Powinno wyjść poprawnie prawda? Sprawdziłem wiele razy i nigdzie nie mam błędu rachunkowego a styczną która wychodzi z tego drugiego przypadku jest styczną na kalkulatorze graficznym tylko do jednego z okręgów

123: Zamiast do obydwu

chichi: podaj polecenie i równania stycznych które otrzymałeś

123: Jest to zadanie z olimpiady nie można

123: Ale takie równanie powinno dać wszystkie 4 styczne prawda?

123: a następnie podstawienie tego drugiego przypadku z wartością bezwzględną do tego drugiego równania

chichi: no to czego tu dziecko szukasz, olimpiada jest dla utalentowanych, a nie tych którzy się forum posiłkują i rozwiązań po necie szukają

123: Mam błąd sam znalazłem spaduwa

123: Zgodzę się z tym nie pytałem konkretnie sam do tego doszddelm