zagadnienia optymalizacyjne Blue: W jakim punkcie krzywej y=x²−1 należy poprowadzić styczną, aby trójkąt ograniczony osiami układu współrzędnych i tą styczną miał najmniejsze pole?

Blue: Pomoże ktoś?

pigor: ..., widzę to tak y=f(x)=x²−1, to f '(x)=2x i f'(x')=2x' i niech (0,a) i (b,0) − punkty wspólne stycznej (*) y=f'(x')(x−x')+y' do paraboli z osiami Ox i Oy w punkcie (x,y)=(x',x'²−1)= ? paraboli, wtedy funkcja pola Δ o którym mowa w zadaniu: (**) P_Δ(x')=¹₂ab , gdzie z (*) a= 2x'(0−x')+x'²−1 i 0= 2x'(b−x')+x'²−1 ⇔ a= −x'²−1 i 2bx'=x'²+1 ⇒ ⇒ b=¹₂x'+¹_2x' , zatem wzór (**) przyjmie postać: P_Δ(x')= ¹₂ (−x'²−1)(¹₂x'+¹_2x')= −¹₄(x'²+1)(x'+¹_{x '}), stąd P_Δ(x')= −¹₄ (x'³+2x'+¹_{x '}) , x'∊R\{0}, no to teraz znajdź minimum lokalne pola tego Δ ze względu na x' − odciętą punktu styczności...

Blue: Trudne to, szczerze mówiąc − średnio rozkminiam...

Blue:

	√3		−2		√3		−2
wychodzi P= (		,		), a w odpowiedziach ma tez odpowiedź (−		,		),
	3		3		3		3

	√3
dlaczego Przecież przy x= −		wychodzi maximum.....
	3

Ktoś mi wyjaśni

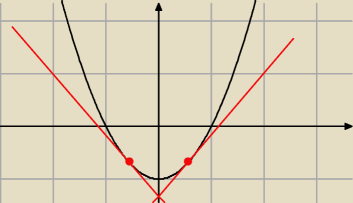
razor: widać?

pigor: ... , lub z parzystości funkcji opisującej krzywą (tu paraboli y=x²−1) można się było tego .... spodziewać .

Blue: no widać i to nawet bardzo logiczne jest, ale jakoś z obliczeń nie wychodzi...

pigor: ..., musi wyjść i z obliczeń (analitycznie), ale mnie nie chce się tego ... liczyć i tyle

Mila: W jakim punkcie krzywej y=x²−1 należy poprowadzić styczną, aby trójkąt ograniczony osiami układu współrzędnych i tą styczną miał najmniejsze pole? f(x)=x²−1 wykres symetryczny względem osi OY P(x₀,y₀) szukany punkt styczności y=f'(x₀)*x+b równanie stycznej f'(x)=2x y=2x₀ *x+b, punkt P należy do wykresu f(x)⇔ x₀²−1=2x₀ *x+b, tąd b=−x₀²−1 Styczna: y=2x₀ *x−x₀²−1 ze względu na symetrię wykresu, rozważę dla x>0 Miejsce zerowe:

	x02+1		x0		1
2x0 *x−x02−1 =0⇔xz=		=		+
	2x0		2		2x0

	x0		1
A(		+		,0)
	2		2x0

Punkt przecięcia osi OY: b b=−x₀²−1

	1		x0		1
PΔ=		*|−x02−1|*(		+		)⇔
	2		2		2x0

	1		x03		1
PΔ=		*(		+x0+		)
	2		2		2x0

	1		3x2		1
P'Δ(x0)=		*(		+1−		)
	2		2		2x02

	3x02		1
(		+1−		)=0⇔ ( dalej piszę x zamiast x0)
	2		2x02

	1		1
(x2−		)*(x2+		)=0⇔
	3		3

	1
(x2−		)=0
	3

	√3		√3
(x−		)*(x+		)=0
	3		3

	√3		√3
x=		lub x=−		∉D
	3		3

	√3		√3
f'(x)>0 dla x>		pochodna zmienia znak z (−) na (+) przy przejsciu przez x=
	3		3

	√3
dla x=		funkcja f(x) ma minimum ( rozważamy f(x) dla x>0)
	3

	√3		√3		√3		3		3		1		2
y=2*		*		−(		)2−1 =2*		−		−1=		−1=−
	3		3		3		9		9		3		3

	√3		2
P1=(		,−		)
	3		3

wobec symetrii wykresu f(x) względem osi OY ma minimum

	√3
dla x=−
	3

	2
y=−
	3

	√3		2
P2=(−		,−		)
	3		3

Mila:

sushi_ gg6397228: olała Ciebie

Mila: Blue, lubi tylko panów.

anna: dziękuję