asymptoty ///: czy jest możliwe aby wykres przeciął asymptotę na poziomą?

ICSP: a co to jest asymptota?

///:

	x
no tak ale mam przykład		granice są w nieskończonościach 0 więc y=0 jest asymptotą i
	1+x2

narysowany wykres przechodzący przez (0,0)

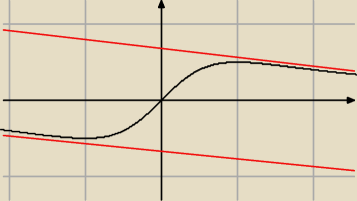
Dziadek Mróz: Co najwyżej czerwone proste są asymptotami ukośnymi

///: w podręczniku asymptota pokrywa się z osią ox zaznaczone miejsce zerowe i zdanie wykres funkcji może mieć punkty wspólne z jego asymptotą poziomą −dlaczego? nic z tego nie rozumiem myślałam że to jest niemożliwe

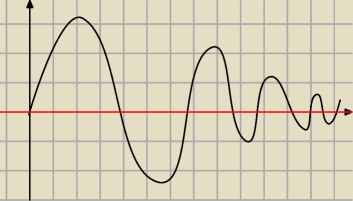
ICSP: czerwona prosta jest asymptotą.

///: no właśnie więc może mieć punkty wspólne a od czego to zależy?

kochanus_niepospolitus: asymptota to jest prosta do której wykres funkcji 'dąży' w +∞ pamiętasz może tw. Cauchiego odnośnie granic ciągów

///: pamiętam, no właśnie dąży przecież generalnie asymptoty to proste do których wykres się zbliża to skąd wiedzieć kiedy przetnie skoro widać że może przecinać

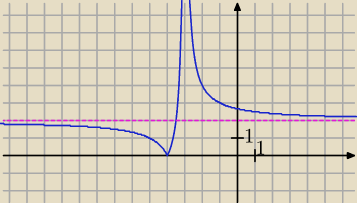
Toskan: To skąd wiedzieć kiedy przetnie? Wtedy wykres funkcji będzie miał punkt wspólny z asymptotą. Zobacz na przykład funkcję:

	2
f(x) = |		+ 2|
	x+3

///: czy to znaczy że pionowa i ukośna też może być przecięta

Toskan: Jeśli chodzi o ukośną Zobacz wykres funkcji w większej skali.

	100 sin x
f(x) = x +
	x

Jeśli chodzi o pionową to może być tak na przykład, że funkcja ma lewostronną asymptotę pionową w punkcie x₀ i zbiega w +∞. Funkcja nie jest ciągła i jest określona w punkcie x₀. tzn ma punkt wspólny z asymptotą pionową lewstronną. Z prawej strony natomiast jest określona i ma tam jakiś wykres. Czyli funkcja posiadałaby jeden punkt wspólny z tą asymptotą. Więcej posiadać nie może bo ty by nie była funkcja.

///: a no tak dzięki za wyjaśnienie