pole obszaru Martyna: Witam Mam takie dane : y= x³ x=−2 x=1 Narysowałam to i wiem ze pkt przecięcia to o −2 i 1 tylko nie wiem co dalej

J: Ja też nie mam pojęcia .

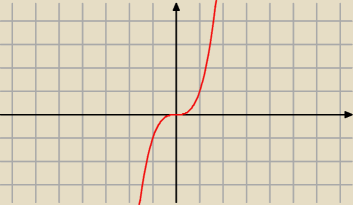
jakubs: y=x³ Jakie punkty przecięcia ?

Martyna: no bo jest jeszcze x= −2 i x=1 myślałam ze to te punkty

J: Przepisz porządnie treść zadania.

Martyna: Oblicz pole obszaru ograniczonego: y= x³ x= −2 x=1

J: No to inna rozmowa ... szukasz punktów przecięcia i liczysz całkę oznaczoną z y = 3 w granicach całkowania <− 2 , 1>

Martyna: no to chyba za tępa jestem bo nie wiem jak szukac pkt przecięcia...

J: Nie musisz... pospieszyłem się z tymi punktami .... tutaj masz już wyznaczone granice całkowania Obliczasz całkę oznaczoną: ∫ x³dx w granicach całkowania od − 2 do 1

Martyna: no tak myślalam ∫ od −2 do 1 3x² tak?

J: To jest pochodna ... a masz policzyć całkę.

Martyna: no tak x⁴/4 dziękuję za cierpliwość

Martyna: − 15/4 mi wyszło mam nadzieję że dobrze

J: OK.

Vizer: Tia ... ujemne pole obszaru.

Martyna: no tak wychodzi

Martyna: J dobrze to jest prawda?

J: Nie dokońca musimy policzyć jeszcze raz ... P₁ = − ∫ x³dx w gracicach: <−2,0> P₂ = ∫ x³dx w granicach : <0,1> i P = P₁ +P−2

Martyna: no tak 0 jest pkt przecięcia z y=x³ a potem mam to chyba odjąć? czy dodać te 2 całki?

J:

	1		15
P1 = 4 , P2 =		i P =
	4		4

J:

	x4
P1 = − [		]o = − [ 0 − 4 ] = − (−4) = 4
	4

J: Krzywa y = x³ w przedziale <−2,0> leży pod osią OX ,stąd minus przed całką.

Martyna: a mi wyszło −4

	x4		04		−24
∫od −2 do 0		dx =		−		= 0−4= −4
	4		4		4

J:

	1		17
No i oczywiście : P = 4 +		=		...
	4		4

Martyna: aha

Martyna:

	1		15		30
rozpisałam to tak: ∫od −2 do 0 − ∫od 0 do 1 + ∫od − 2 do 1 = 4 −		+		=
	4		4		4

J: Nie ... popatrz na post: 16:58

Martyna:

	1
no ja rozumiem że p1= 4 p2 =		i mam to tylko dodać i jest koniec?
	4

J: Tak.