pole obszaru Zagubiona: Mam obliczyć pole obszaru ograniczonego liniami: 4y=8x−x² i 4y=x+6 8x−x² = x+6 x² − 7x + 6 = 0 x=1 i x=6

	8x − x2 − x − 6
∫
	4

no i nie wiem co dalej

wredulus_pospolitus: hęęęę

wredulus_pospolitus: w sumie dobrze jest ale jakoś tak dziwnie mi się wydawało pamiętaj o 'dx' przy całce

J:

	8x − x2		x+6
= ∫		dx − ∫		dx = ... ( w granicach całkowania <1,6> )
	4		4

Zagubiona:

	8x−x2		8x		x2
∫		dx=		−		dx
	4		4		4

	1
∫2x−		x2
	4

	1		x3
x2 −		*
	4		3

czy mam to policzyć przez podstawianie? Już się pogubilam

wredulus_pospolitus: dobrze ... podstawienie zbyteczne ... to są całki 'elementarne'

Zagubiona:

	860
Wynik wyszedł mi		. Mógłby ktoś sprawdzić?
	96

Mila:

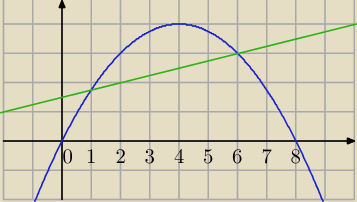
	1
y=2x−		x2
	4

	x		6
y=		+
	4		4

granice calkowania 0d (1) do (6)

	1		x		6
1∫6(2x−		x2−		−		)dx=
	4		4		4

	1		7x		3		1		7		3
=1∫6(−		x2+		−		)dx=[−		x3+		x2−		x]16=
	4		4		2		12		8		2

	1		7		3		1		7		3		125
=−		*216+		*36−		*6+		−		+		=
	12		8		2		12		8		2		24