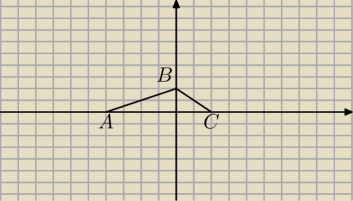
Oblicz całkę podwójną filmorf: Oblicz całke podwójna ∫∫(1+x−y)dxdy pole jest ograniczone trójkątem o wierzchołkach A(−4,0); B(0,2); C(2,0) prosta AB: prosta AC prosta BC

	⎧	b=2
y=ax+b y=0	⎩	0=2a+b

⎧	2=b
⎩	0=(−4a)+b	−2a=2

4a=2 a=−1 a=¹₂ y=2−x y=¹₂x+2 więc rozbijam to na dwa obszary ∫dx ∫(1+x−y)dy x<−4,0> y<0,¹₂x+2> + ∫dx ∫(1+x−y)dy x<0,2> y<0;2−x> No i po obliczeniach (kilkukrotnych) wychodzi mi w pierwszej −4, a w drugiej 2, czyli po zsumowaniu −2, natomiast w odpowiedziach jest 2. Ktoś mi jest w stanie wyjaśnić czemu tak?

wredulus_pospolitus: pokaż obliczenia

filmorf: ∫(1+x−y)dy = y+xy−¹₂y²+c <0;¹₂x+2> (¹₂x+2)+x(¹₂x+2)−¹₂(¹₄x²+4+2x)=¹₂x+2+¹₂x²+2x−¹₈x²−2−x = ³₂x+³₈x² ∫(³₂x+³₈x²)dx=³₄x²+¹₈x³+c <−4,0> 0−[12−8]=−4 ∫(1+x−y)dy = y+xy−¹₂y²+c <0,2−x> 2−x+x(2−x)−¹₂(4−4x+x²)=2−x+2x−x²−2+2x−¹₂x²=3x−³₂x² ∫(3x−³₂x²) dx=³₂x²−¹₂x³ <0;2> 6−4−[0]=2

filmorf: dobra już widzę swój błąd, zapomniałem o dolnych (zero) granicach całkowania

filmorf: albo nie, chyba dobrze to jest, niech ktoś miły to jeszcze sprawdzi bo już się gubię

aniołek: up

Mila: sprawdzam.

Mila: Mam takie wyniki, jak Twoje. zastanawiam się dlaczego masz inny wynik w odpowiedzi, czy dobrze przepisałeś przyklad?

filmorf: Dobrze przepisałem. Może skoro pierwsza całka wyszła ujemna to jej się nie powinno brać pod uwagę, albo z końcowego wyniku obliczyć wartość bezwzględną.