Oblicz prawdopodobieństwo john2: Witam. Proszę o sprawdzenie zadania z prawdopodobieństwa. Dwóch rewolwerowców strzela raz jednocześnie w bandytę. Niech A oznacza trafienie bandyty przez pierwszego rewolwerowca, zaś B − trafienie bandyty przez drugiego rewolwerowca. Zdarzenia te są niezależne. Prawdopodobieństwo trafienia pierwszego rewolwerowca wynosi 0,2, natomiast drugiego 0,3. Oblicz prawdopodobieństwo tego, że: a) bandyta zostaje postrzelony raz b) bandyta zostaje postrzelony raz lub dwa razy a) Liczę P(A∪B), czyli trafia rewolwerowiec 1 lub drugi: P(A∪B) = P(A) + P(B) − P(A∩B) = 0,2 + 0,3 − 0,2 * 0,3 = 0,44 b) Liczę P[(A∪B)∪(A∩B)], czyli szansa, że trafi jeden albo drugi lub jeden i drugi: P[(A∪B)∪(A∩B)] = P(A∪B) + P(A∩B) − P[(A∪B)∩(A∩B)] = 0,44 + 0,06 − 0 = 0,5 Zadanie wymyśliłem, więc może być bez sensu.

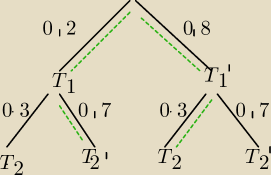
Mila: a) A − cel trafiony raz P(A)=0,2*0,7+0,8*0,3=0,14+0,24=0,38 b)B− cel trafiny raz lub dwa razy B'− cel nie zostaje trafiny ani raz P(B')=0,8*0,7=0,56 P(B)=1−0,56=0,44

john2: Dziękuję bardzo.

Mila: