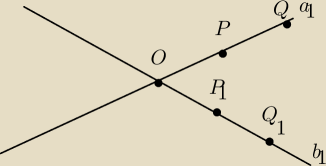
izometria 5-latek: 1.OP=OP₁ i OQ=OQ₁ z alozenia i konstrukcji 2.OP+PQ=OQ 3.OP₁+PQ=OQ₁ 4.OP₁+P₁Q₁= OQ₁ lub OQ₁+Q₁P₁= OP₁ W 1 przypadku punkt P₁ lezy miedzy punktami Oi Q₁ W drugim przypadku Q₁ lezy miedzy O i P₁ W 1 przypadku 5. P₁Q₁=PQ z rownosci 4 i 3 W drugim przypadku 6. PQ+P₁Q₁=0 co jest niemozliwe O ile pierszy przypadek rozumiem bo jesli te dwa rownania maja byc rowne to P₁ Q₁ musi rownac sie PQ natomiast 2 pzypadek juz nie bardzo dlaczego PQ+P₁Q₁ =0 czy to wynika z tego ze ? OQ₁+P₁Q₁= OP₁ OP₁+PQ= OQ₁ i teraz po dodaniu stronami wyjdzie OQ₁+OP−1+P₁Q₁+PQ=OP₁OQ₁ Teraz P₁Q₁+PQ=0 ? Udowadniam ze przeksztalcenie okreslone w ten sposob Punktowi O przyporzadkujemy punkt O .Kazdemu punktowi P nie rowna sie O polprostej a₁ − punkt P₁ polprostej b₁ taki ze OP₁=OP jest izometria .

5-latek: Bo chyba nie chodzi tu o to ze w drugim przypadku punkt P₁ pokryje z sie punktem Q₁ i wtedy odleglosc miedzy nimi =0

wredulus_pospolitus: punkt 3. −−− to nie jest prawda

wredulus_pospolitus: 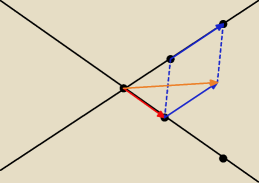ten wektor otrzymujesz z sumy wektorów OP₁ i PQ

wredulus_pospolitus: czy tu 'jedziesz' na długościach nawet jeśli to ta równość pokazuje, że ΔOQQ₁ i ΔOPP₁ są to trójkąty równoboczne

5-latek: Witaj Artur Przepraszam ze nie odpisywalem bo musialem wyjechac . Ale ta rownosc 3 wynika z rownosci 2 i 1 tak chodzi o odleglosc tych obrazow (czyli dlugosc Wiec jesli tu spojrzysz jeszce to podpowiedz mi czy ta wiadomosc o trojkatach rownobocznych przyda sie do takiego zadania z tego paragrafu Wykazac ze w izometrii wnetrze trojkata przeksztalca sie na wnetrze odpowiedniego trojkata Wnetrze trojkata to wiadono (bez lamanej ABC Wroce wieczoren z pracy to zobacze . dzieki

5-latek: JUtro jest Swieto to poczytam sobie w spokoju .Obrazy niektorych figur w izometrii ( obraz odcinka , polprostej prostej ,kąta wypuklego i wkleslego , okregu) takze o figurach przystajacych

wredulus_pospolitus: ach ... tam jest OQ₁ ... a ja widziełem QQ₁

5-latek: Wiesz na drugi raz nie bede pisal podobnych liter . Bede np pisal PX (moglo zmylic−przepraszam A o tym trojkacie rownobocznym ?

5-latek: Mam jeszce prosbe . Moze Ty to mi wytlumaczysz Mam takie zadanie . Figura skladasie z 5 punktow A B C D E . Okreslamy przeksztalcenie geometryczne T tak T(A)=B , T(B)=C T(C)=A T(E)=D T(B)=E Uzasadnij z e przeksztalcenie T jest odwracalne .

5-latek: wedlug mnie nie jest bo np B jest w tym przeksztalceniu obrazem punktu A wiec jesli ma byc odwracalne to A bedzie obrazem punktu B a obraze punktu B jest punkt C i E (Nie wiem vczy dobrze mysle

wredulus_pospolitus: źle .... odwracalne przekształcenie jest to takie że z wyniku można dojść do danych poczatkowych, więc: T⁻¹(B)=A T⁻¹(C)=B T⁻¹(A)=C T⁻¹(D)=E T⁻¹(E)=D druga sprawa −−− kiedy istnieje funkcja odwrotna (odwzorowanie odwrotne do funkcji) ? Gdy funkcja jest różnowartościowa i 'na' ... zaimplementuj te warunki do Twojego zbioru (w końcu funkcja to nic innego jak zbiór nieskończonej liczby punktów) i masz 'różnowartościowość' i 'na' w tym zbiorze, więc istnieje przekształcenie odwrotne

5-latek: Autor podaje tak. . Przeksztalcenie T' figury F na F' nazwiemy jednoznacznie odwracalnym lub krotko odwracalnym jezeli do kazdego punktu P' figury F' mozna wskazac jeden i tylko jeden punkt P figury F ktorego obrazem w przeksztalceniu T jest punkt P' .

wredulus_pospolitus: mało tego ... de facto zrobienie 5razy przekształcenia T, jest de facto przekształceniem odwortnym w końcu: '0' 1 2 3 4 5 T(A) = B −> T(B) = C −> T(C) = A −> T(A) = B −> T(B) = C −> T(C) = A T(B) = C −> T(C) = A −> T(A) = B −> T(B) = C −> T(C) = A −> T(A) = B T(C) = A −> T(A) = B −> T(B) = C −> T(C) = A −> T(A) = B −> T(B) = C T(E) = D −> T(D) = E −> T(E) = D −> T(D) = E −> T(E) = D −> T(D) = E T(D) = E −> T(E) = D −> T(D) = E −> T(E) = D −> T(D) = E −> T(E) = D

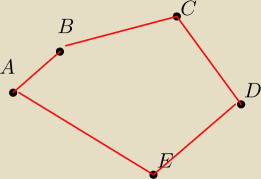
5-latek: Powiedzmy ze jst taka figura . Mozesz to zobrazowac na tym rysunku (jesli sie da . Ja juz ciezko mysle i niektore rzeczy muszse kilka razy przemyslec BYc moze ze autor juzzaklada w tym momencie ze pojecie funkcji odwortnej powinno byc znane (jest to ksiazka do klasy 1 technikum (1970r

5-latek: Teraz po Twoim rozpisaniu to stalo sie jasne . dziekuje CI bardzo . Zaraz to sobie zapiszse i wydrukuje