badanie funkcji aa: Mam do zbadania funkcje:

	√x3
f(x)=
	√x−1

Znam caly schemat badania przebiegu funkcji, ale pojawil sie problem juz na poczatku, a mianowicie przy wyliczaniu dziedziny: D_f: x−1≠0 ⇒ x≠1

x3
	≥0 ⇔ x3≥0 ⋁ x−1≥0
x−1

x≥1 v x≥0 D_f: x∊(1,∞) Tylko kiedy generuje taki wykres w wolfram alpha: http://www.wolframalpha.com/input/?i=f%28x%29%3Dsqrt%28x%5E3%2F%28x-1%29%29 to okazuje sie, ze D_f: x∊(−∞,0)∪(1,∞). Gdzie popelniam blad?

ICSP: źle wpisałęś/aś funkcje do wolframa.

ICSP: http://www.wolframalpha.com/input/?i=f%28x%29%3Dsqrt%28x%5E3%29%2Fsqrt%28x-1%29%29

aa: * D_f: x∊(−∞,0]∪(1,∞)

aa: przepraszam, to tu zle wpisalam funkcje:

	x3
f(x)=sqrt(		)
	x−1

J: Widzę,że Twoja procedura ... to wolframalpha .... a sam nie potrafisz wyznaczyć dziedziny

ICSP:

	x3
D :		≥ 0 ⋀ x − 1 ≠ 0
	x −1

aa: poza tym chyba to jest to samo

J: Twoje wyznaczanie dziedziny ... to KATASTROFA .. brak elementarnej wiedzy.

aa: w pierwszym poscie wyliczylam dziedzine, sprawdzam czesto wyniki w wolframie, to chyba nic zlego i po prostu zastanawiam sie gdzie robie blad

aa: J, w takim razie mozesz mi pomoc skoro wyznaczasz dziedzine lepiej

aa: chyba od tego jest to forum: od pomagania sobie nawzajem

J: Dokładnie tak, jak Ci napisał "ICSP" ...., czyli : x³(x − 1) ≥ 0 i x − 1 ≠ 0

aa: prosze wytlumaczenie mi dlaczego mi dziedzina wyszla x∊(1,∞), a powinno byc x∊(−∞,0]∪(1,∞). bardzo mozliwe, ze popelnilam gdzie po prostu glupi blad i nie potrafie tego dostrzec (tak to bywa z glupimi bledami)

aa: no to na to sama juz wpadlam, wszystko to rozpisalam w pierwszym poscie

aa: zatem, drogi/a J pokieruje sie wskazowkami ICSP, czyli innymi slowy: POWTORZE to co SAMA napisalam w PIERWSZYM poscie (to ten na samej gorze ):

	x3
jezeli mam		≥0, czyli to co napisalam w PIERWSZYM poscie, to:
	x−1

x³≥0 ⇔ x≥0 x−1≥0 ⇔ x≥1 x≠1 stad dziedzina wychodzi mi x∊(1,∞), czyli znow nie tak jak na wykresie. gdzie lezy moj blad? a moze go nie ma tylko wolfram ma kiepski algorytm (w co MOCNO watpie)

aa: * x≠1 jest dla warunku x−1≠0 tak dla scislosci bo zapomnialam dopisac

J:

	a
W pierwszym poście napisałaś bzdury ... wynika z nich ,że jeżeli :		≥ 0 ⇔
	b

a≥0 lub b≥0 .. bzdura

J:

	a
Droga "aa" ...		≥ 0 ⇔ a ≥ 0 i b ≥ 0 lub a ≤ 0 i b ≤ 0
	b

aa: no i bardzo dziekuje, bo wlasnie uswiadomiles/as mi moj blad! tylko moglo sie to odbyc bez wytykania mi, ze nie mam elementarnej wiedzy, ze moje obliczenia to katastrofa, albo powtarzanie po kilka razy "bzdura" naprawde wystarczyloby: spojrz uwaznie na warunki i zastanow sie jeszcze raz.

J: Nie obrażaj się ... nie chciałem Cię urazić ..

aa: luzik, czesto spotykam sie z takim odpowiadaniem na tym forum, wiec mozna powiedziec, ze juz przywyklam, ale uwazam, ze to mimo wszystko jedno z lepszych miejsc w sieci na pytania w kwestii matmy studiuje fizyke, wiec w matmie czasem sie gubie na glupotach, aczkolwiek rzadko mi sie to zdarza. jeszcze raz dzieki za odp, zapisze sobie to na czole

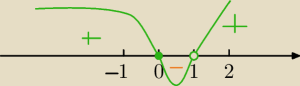
Mila: Rozwiązuj nierówność standardowo. x³*(x−1)≥0 x=0, x=1 miejsca zerowe⇔ patrz na oś x≤0 lub x>1