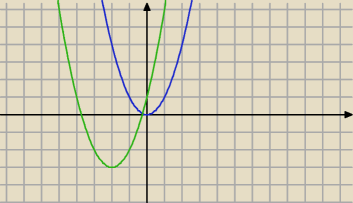
A#4 Lukas: Uzasadnij, że parabola p o równaniu y=x² jest przystająca do paraboli a) y=x²+4x+1 Po za rysunkiem zauważyłem tylko że parabola y=x²+4x+1 jest przesunięta o wektor [1,3] ?

?: Translacja jest izometrią , wniosek ......

Lukas: Parabole są przystające, dziękuję musiałem się upewnić.

?: Jak wyznaczyłeś współrzędne wektora ? y=x²+4x+1= (x+2)²−3 , u=[−2,−3]

Lukas: Policzyłem kratki

?:

Lukas: zad 2 Punkt A=(12,6) przekształcono w jednokładności o środku S i skali k Znajdź wsp. obrazu punktu A S=(−7,5) k=1 Jak to zapisać ?

?: Dla k=1 A=A^'

Lukas: a np dla k=−2 ale to się jakoś zapisuję za pomocą wektorów ?

?: → → SA^'= k*SA , A^'(x,y)

jakubs: Mila ostatnio podawała Ci wzorki na jednokładność.

Lukas: A jak zapisać wektor SA.? Podawała wzory,ale nie jak zapisać to wektorowo. [x+7, y−5]=−2[ ? ? ? ?]

zawodus: Nie wiesz jak się oblicza współrzędne wektora?

?: [x+7], y−5]= −2[12+7, 6−5] ⇒

Lukas: Już wiem

?: S(a,b) − środek jednokładności , k≠0 − skala jednokładności A(x,y)− dany punkt A^'(x^',y^') − punkt po przekształceniu {x^'=k*(x−a)+a A^' : {y^'=k*(y−b)+b

Lukas: Dziękuję