monotonicznosc i ekstrema kfiatek: Zbadaj monotonicznosc i ekstrema: f(x)=|x−1| D_f: x∊R taak, wiem, funkcja niezbyt trudna wiem, ze trzeba rozbic na dwa przypadki y₁=1−x y₂=x−1 licze pochodne y'₁=−1 i y'₂=1, tylko, ze teraz trzeba je przyrownac do 0... mam na wykresie narysowac po prostu, ze sa to dwie funkcje stałe jedna y=−1, a druga y=1? I czy funkcje y₁ i y₂ mam traktowac w ogole jak dwie odrebne funkcje, dla ktorych beda osobne rozwiazania? Prosze o podpowiedz

WueR: Czy w ogole zdajesz sobie sprawe z tego, czym jest pochodna?

Metis: https://matematykaszkolna.pl/strona/381.html

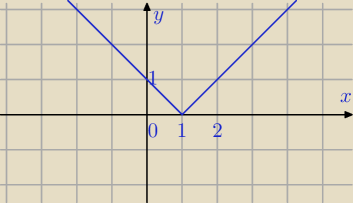
Mila: Nie strzelaj do wróbla z armaty. y=|x−1| i wszystko widzisz.

kfiatek: WueR, wydaje mi sie, ze zdaje sobie sprawe z tego, czym jest pochodna, bo, w przypadku ekstremow i monotonicznosci na przyklad, przy pomocy jej znaku okreslam czy funkcja rosnie, czy maleje Mila, wlasnie sie zastanawialam, czy za bardzo nie kombinuje, ale ten przyklad znalazl sie posrod kilkunastu innych trudniejszych i jak widac "troche" mnie zmylil dzieki bardzo za oswiecenie

kfiatek: Metis, tak, znam te zaleznosci w linku, ktory podrzuciles

WueR: No tak, ale czy wiesz, dlaczego monotonicznosc okresla sie za pomoca znaku pochodnej? Dla Twojego przykladu, skoro w jednym przedziale pochodna wyszla 1, to powinienes juz wiedziec, ze na tymze przedziale funkcja jest rosnaca. A tam rowniez nie okresliles, w jakich przedzialach dokladnie funkcja ma pochodna [a tutaj akurat kosa trafila na kamien i ekstremum jest w punkcie, w ktorym pochodnej nie ma].

kfiatek: Jezeli funkcja jest okreslona i rozniczkowalna na danym przedziale, a jej pochodna w kazdym punkcie tego przedzialu jest dodatnia/ujemna, to funkcja jest na tym przedziale rosnaca/malejaca. Tyle pamietam z wykladu. Czy jesli chodzi o sprawdzenie, gdzie funkcja ma pochodna, mam skorzystac ze wzoru:

	f(x0+Δx)−f(x0)
lim(Δx→x0+/−)
	Δx

gdzie w tym przypadku x₀=1? I czy bedzie to Δx→1− dla 1−x, a Δx→1+ dla x−1? Jesli cos pogmatwalam, to prosze o poprawienie

Wazyl: kfitek jeżeli policzyłeś pochodne i okazało się że w żadnym punkcie dziedziny się nie zerują pytanie czy ta funkcja ma ekstremum? A jeżeli tak to z czego to wynika?

kfiatek: juz ktoras osoba pisze czy policzyłEM pochodne, wiec pozwole sobie juz poprawic: owszem, policzyłAM a odpowiadajac na pytanie − patrzac na wykres, ktory podała mi Mila to wydaje mi sie ze w P(1,0) funkcja ma ekstremum a konkretnie minimum. I tyle jestem w stanie powiedziec.

WueR: Po pierwsze nalezalo by dobrze napisac jak ta funkcja wyglada: f(x) = x − 1 dla x ≥ 1 i 1 − x dla x < 1 Dosc oczywistym jest, ze funkcja na przedzialach (−∞,1) oraz (1,∞) jest rozniczkowalna, ale w punkcie x = 1 juz nie [dowod − policzyc pochodne jednostronne w tym punkcie]. Ale owszem, ma tam ekstremum, jak to juz latwo intuicyjnie okreslic na podstawie wykresu. Wazne, zeby na poczatku okreslic, gdzie dokladnie funkcja jest rozniczkowalna i w przypadku szukania ekstremum sprawdzic rowniez punkty watpliwe, tzn. te, ktore wypadly z dziedziny pochodnej − bo podejrzane o bycie ekstremum sa nadal.

kfiatek: czyli zeby sprawdzic rozniczkowalnosc tej konkretnej funkcji musze obliczyc lim_x→1− 1−x i lim_x→1+ x−1 ? czy tak?

kfiatek: tylko hmm... jakbym policzyla to co napisalam to i tu i tu wyjdzie 0. czyli to jednak nie tak (?)

WueR: Nie, trzeba z definicji pochodnej jednostronnej sprawdzic, co sie dzieje w obu przypadkach.

kfiatek: Czyli z tego wzoru, ktory napisalam kilka postow wyzej? (Ten z Δx).

WueR: Zgadza sie.

kfiatek: rany, dzieki wielkie chyba zapamietam to do konca zycia...