A#4
Lukas:
Jak sprawdzić czy przekształcenie płaszczyzny jest izometrią ?
P=((x,y))=(−x,y+1)
Wskazówki ?
15 cze 17:10
zawodus: Przekształcenie jest izometrią, jeśli zachowuje odległość punktów.
Tego nie ma w podstawie programowej dla liceum
15 cze 17:17
Lukas:
Ale to zadanie z A.Kiełbasy
15 cze 17:18
Mila:
Izometria zachowuje długości odcinków.
A=(xa,ya), B=(xb,yb) dowolne punkty płaszczyzny
|AB|=√(xb−xa)2+(yb−ya)2
Znajdź obrazy tych punktów i zbadaj, czy :
|AB|=|A'B'|
15 cze 17:20
Lukas: obraz względem czego ?
15 cze 17:21
Mila:
No masz podane przekształcenie.
P(x,y)→P'(−x,y+1)
x przyporzadkowano (−x)
y przyporządkowano (y+1)
A(xa,ya) dany punkt
A'(−xa,ya+1)
B'(−xb,yb+1)
teraz oblicz :
|A'B'|
15 cze 17:45
Lukas:
|A'B'|=√(−xb+xa)2+(yb+1−ya−1)2
15 cze 17:47
Mila:
=√(xb−xa)2+(yb−ya)2=|AB| to przekształcenie jest izometrią .
Abys lepiej zrozumiał, zrób to dla konkretnych dwóch punktów:
A=(1,2) , B=(6,4)
15 cze 17:58
Lukas:
A jakie równanie płaszczyzny ? Takie samo ?
15 cze 18:00
Mila:
Po co równanie płaszczyzny ?
Przekształcenie to samo.
15 cze 18:06
Lukas:
|AB|=√(1−6)2+(2−4)2
|AB|=√29
|A'B'|=√(−1−6)2+(3−5)2
|A'B'|=√53
15 cze 18:12
Mila:
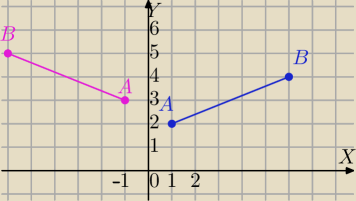
A'=(−1, 3)
B'=(−6,5)
|A'B'|=
√(−6+1)2+(5−3)2=
√25+4=
√29
To przekształcenie jest złożeniem dwóch izometrii,
symetrii S
OY i translacji T[0,1]
15 cze 18:28
Mila:
To ładne zadanie dla 5−latka, bo właśnie zajmuje się przekształceniami.
Może tu spojrzy.
15 cze 18:30
Lukas:
Ja wgl tej izometrii jakoś nie czuję
15 cze 18:39
Mila:
Zobacz na rysunku otrzymałeś odcinek tej samej długości, tylko w innym miejscu.
Poznane izometrie:
Symetria osiowa
symetria środkowa
translacja
obrót
Jednokładność dla k≠1 i k≠−1 nie jest izometrią .
15 cze 18:53
Lukas:
Właśnie ze symetrii to byłem słaby, zawsze wolałem bryły.
15 cze 18:59
Lukas:
Czyli po prostu jest izometrią...
15 cze 20:02
Mila:
Dane przekształcenie jest izometrią.
|AB|=|A'B'|
15 cze 20:04
Lukas:
Dziękuję.
15 cze 20:07
Mila:
15 cze 20:08