Jaka pochodna? Łukasz:

	x
y=x+
	x−1

pochodna z tego to:

	1(x−1)−x
1+
	(x−1)2

nie wiem czy dobrze to mam?

ICSP: Jeszcze to uprość

Dziadek Mróz:

	x
y = x +
	x − 1

	x(x − 1) + x
y =
	x − 1

	x2
y =
	x − 1

	u
y =		u = x2 v = x − 1
	v

	u		u'v − uv'
y' = [		]' =		= (1) ...
	v		v2

u' = [x²]' = 2x v' = [x − 1]' = 1

	2x(x − 1) − x2		2x2 − 2x − x2
... (1) =		=		=
	(x − 1)2		(x − 1)2

	x2 − 2x		x(x − 2)
=		=
	(x − 1)2		(x − 1)2

Łukasz: ok, a extrema lokalne i pkt. wypukłości da się z tego zrobić? Bo wynika, że x=0 lub x=−2 to teraz liczę drugą pochodną i robię f"(−2)

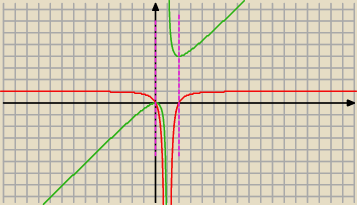
asdf: ekstrema lokalne, czy gdy pochodna jest rowna zero:

x(x−2)
	= 0 => x(x−2) = 0 => x= 0 v x = −2
(x−1)2

czerwony − wykres pochodnej zielony − wykres funkcji

asdf: obliczenie rownosci: x(x−2) = 0

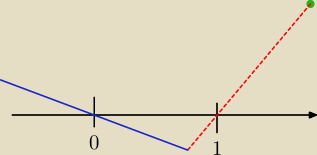
asdf: punkt przegiecia to punkt, gdy pochodna z pochodnej zmienia swoj znak, czyli w punkcie x = 0, musisz wiec policzyc:

	x(x−2)
(		)' = ....
	x−1)2

pozniej przyrownac do zera itd...jakbys obejrzal filmiki bys wiedzial, nie wspomnialem tutaj o kilku waznych rzeczach, czyli o krotnosci pierwiastka, np. x(x−1) = 0, x = 0 (pierwiastek jednokrotny), x = 1(tez) liczysz: lim_x−>∞ x(x−1) = ∞, a wiec rysujesz od gornego, prawego rogu (kropka zielona zaznaczona na rysunku) nastepnie widzisz, ze 1 to pierwiastek nieparzysty (jednokrotny), a wiec przebicina os (jak to pokazano na czerwonym, przerywanym odcinku) teraz masz 0, zero tez jest pierwiastkiem nieparzystym, czyli tez przecinasz os (niebieska ciagla) dla argumentow > 0 (czyli 1 do nieskonczonosci) funkcja jest rosnaca, ponizej zera jest malejaca a w punktach, gdzie ma wartosc 0 i z prawej strony jest dodatnia, a z lewej ujemna (lub na odwrot) to funkcja ma w tych miejscach swoje ekstrema przeanalizuj to dokladnie.

Łukasz: czyli co z tego wynika? że gdzie jest maximum czy minimum?

Łukasz: ok, nie zauważyłem powyższej odp.

asdf: http://www.matemaks.pl/wielomiany.php?tid=1714 dobrze to ogarnij, bo bez tego ani rusz...

asdf: przeczytaj tez tamta uwage ( co jest na samym dole ).