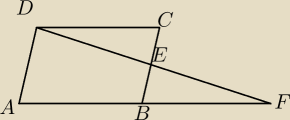
Sprawdzenie czy dobrze zrobiłem zadanie K#62;G#62;: Dany jest równoległobok ABCD (rysunek) . Punkt E jest środkiem boku BC, a punkt F − punktem przecięcia prostych AB i DE . Wykaż że pole trójkąta AFD i równoległoboku ABCD są równe. To co na razie udało mi się ustalić : Δ DEC ≡ ΔBEF

sushi_ gg6397228: i już prawie jest rozwiazane

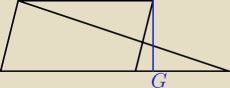
K#62;G#62;: Wiem tez że pole tych figur wyglądają tak mniej więcej . P_AFD = |AF| * |GC| / 2 P_ABCD = |AB| lub |DC| * |CG| Czyli mają takie same wysokości

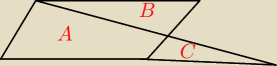
sushi_ gg6397228: B=C pole równoległoboku= A+B pole trójkąta = A+C zatem....

K#62;G#62;: Aha zatem P_AFD = P_ABCD gdyż B=C

K#62;G#62;: kurcze byłem blisko czyli nadal głupi jestem dzięki za pomoc

sushi_ gg6397228: jak trojkaty sa przystajace, to pola sa takie same

K#62;G#62;: No tak "W geometrii figury tego samego kształtu i rozmiaru nazywamy przystającymi " Szkoda że teraz to doczytałem