Całka podwójna po obszarze D MaRKaW: Witam, z racji, że nie mogę dać sobie rady z przykładem proszę was o pomoc. Oto zadanie Oblicz ∬xdx, gdzie D jest obszarem ograniczonym parabolą y=x²+4x i prostą y=x+4

sushi_ gg6397228: zapisz swoje rozwiazanie + rysunek

MaRKaW: https://www.dropbox.com/s/8n45z7zmrmew56h/IMG_20140614_211354.jpg https://www.dropbox.com/s/1gtllhd1cxcg7xs/IMG_20140614_211415.jpg

sushi_ gg6397228: tutaj a nie w linku

daras: sadysta

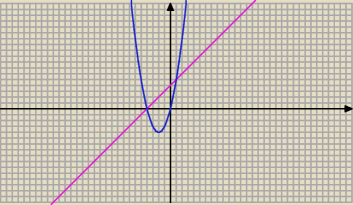
MaRKaW: Punkty przecięcia z osią 0x: (−4;0),(0;0) Wierzchołek paraboli (−2;−4) Miejsca przecięcia wykresów: (−4;0),(1;5) −4≤x≤1 −4≤y≤x²+4x _D∬xdx po obszarze D ₋₄∫¹dx[₋₄∫^x2+4xxdy] ∫xdy=x∫dy=xy +c podstawienie granic x*(x²+4x−4)=x*(x+2)² ∫x*(x+2)²dx podstawienie t=x+2 dt=dx x=t−2 ∫(t−2)*t²dt = ∫t³−2t²dt = ∫t³dt −2∫t²dt = ¹₄t⁴ − ²₃t³+c = =¹₄(x+2)⁴ − ²₃(x+2)³+c podstawienie granic (¹₄3⁴ − ²₃3³) − (¹₄(−2)⁴ − ²₃(−2)³) = =(⁸¹₄ − ⁵⁴₃) − (4 + ¹⁶₃)= =²⁷₁₂ − ²⁸₃ = ²⁷₁₂ − ¹¹²₁₂ = −⁸⁵₁₂

MaRKaW: i co w tym źle robie?

sushi_ gg6397228: trzeba podzielic obszar na 3 pola i dopiero go ograniczyć

sushi_ gg6397228: poza tym x²+4x−4 ≠(x+2)²

MaRKaW: tam + jest, pomylka przy przepisywaniu x²+4x−(−4)