zadania, prostopadłościany. Filip: Mam 3 zadanka, potrzebuje ich jak najszybciej! byłbym wdzięczny za pomoc, proszę o rozwiązanie po kolei, tak żebym wiedział co robię. Z góry dziękuje! 1.Suma długości wszystkich krawędzi graniastosłupa prawidłowego sześciokątnego jest równa 96 cm. Jakie wymiary powinien mieć ten graniastosłup, aby jego objętość była największa? 2.Dany jest prostopadłościan o krawędziach x, x+3, 3−x. Dla jakiej wartości x, objętość prostopadłoscianu jest największa. 3.jakie jest największe możliwe pole prostokąta , którego dwa wierzchołki należą do osi x, a dwa pozostałe do paraboli y = 6−x², gdzie y>o² ( lub a², nie mogę się rozczytać)

sushi_ gg6397228: 1. policz ile jest wszystkich krawędzi

PW: 2. V(x) = x(x+3)(3−x), x∊(0,3) − badać, czy i w jakim punkcie funkcja V ma maksimum lokalne na (0, 3). Najprościej będzie wymnożyć i liczyć pochodną wielomianu trzeciego stopnia.

Tadeusz: 1. 12a+6h=96 ⇒ 2a+h=16 ⇒ h=16−2a

	a2√3
Pp=6*
	4

	a2√3
V=6*		h V=1,5a2√3(16−2a) ⇒ V=24√3a2−3√3a3
	4

V'=48√3a−9√3a² V'=0 a√3(48−9a)=0 itd

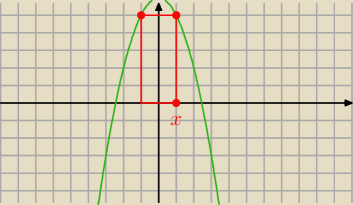
Tadeusz: P=2x(6−x²) ⇒ P=−2x³+12x P'=−6x²+12 itd