Oblicz całkę oznaczoną
Anikka04: Oblicz całkę oznaczoną:
∫cosxdx na zb x∊(−π/2;π/2)
14 cze 18:05
J: Przecież to całka elementarna.
14 cze 18:06
zombi: Serio?
14 cze 18:10
J: Nie...żartowałem..

14 cze 18:11
zombi: To było do niej

14 cze 18:16
Mila:
O co Ci chodzi zombi?
14 cze 18:17
J: 
14 cze 18:17
Anikka04: ktoś mógłby mi to rozpisać?
14 cze 18:26
Anikka04: cos2x,
sorry mój błąd
14 cze 18:27
J: To jest dalej całka elementarna ...

14 cze 18:28
Anikka04: wiem, korzysta się z 1 tryg i z cos2x, ale podstawiam i wychodzi mi 0, nie widzę gdzie robię
błąd
14 cze 18:29
Mila:
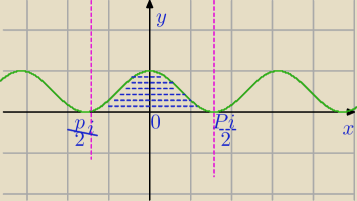
| | 1 | | 1 | | 1 | | 1 | | 1 | |
∫cos2x dx= |
| ∫(cos(2x)+1) dx= |
| *( |
| sin(2x)+x)= |
| sin(2x)+ |
| x |
| | 2 | | 2 | | 2 | | 4 | | 2 | |
−π2∫
−π2cos2x dx=
| | 1 | | π | | 1 | | π | | 1 | | −π | | 1 | | π | |
=[ |
| sin(2* |
| )+ |
| * |
| − |
| sin(2* |
| )− |
| *(− |
| )= |
| | 4 | | 2 | | 2 | | 2 | | 4 | | 2 | | 2 | | 2 | |
14 cze 19:07
Mila: | | π | |
Górna granica całkowania : |
| |
| | 2 | |
14 cze 19:10
Anikka04: Dziękuję Mila

14 cze 20:39
Mila:

14 cze 20:57






