Trygonometria - parametry Suweren: Wyznacz wartości parametru m (m∊R) dla których równanie: a) sinx=m²−3 ma 3 rozwiązania w przedziale <0, 2π> b) |cosx|=m²−4(m+1) ma 3 rozwiązania w przedziale <0, π> Podobne zadania umiem rozwiązać, ale nie rozumiem o co chodzi z 3 rozwiązaniami w przedziale.

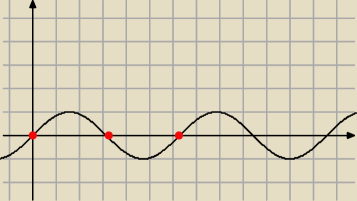
J: Przyłóż linijkę (równolegle do osi OX) i zobacz kiedy ma 3 punkty wspólne z y =sinx w przedziale <0,2π>

Suweren: W zerze. W odpowiedziach jest m = pierwiastek z 3 i pierwiastek z minus 3.

Suweren: Sprawdziłem, przedział jest dobrze przepisany.

razor: a) sinx = m²−3 będzie miało 3 rozwiązania w przedziale <0,2π> wtedy gdy sinx = 0, czyli m² − 3 = 0 ⇔ m² = 3 ⇔ m = √3 lub m = −√3

Suweren: Słodki Jezu, jestem idiotą, to takie proste... Wielkie dzięki.

Suweren: Z całego zestawu zadań nie wyszło jedynie |tgx−1|=m²−6m |tgx−1)=m²−6m ma 2 rozwiązania w przedziale <0,2π> wtedy gdy |tgx−1|>0 Z tego mam przedział (−nsk; 3 − √10) ∪ (3 + √10 ; nsk) W odpowiedzi jest (3 − √10 ; 0) ∪ (6; 3 + √10 ) Jest ktoś chętny wskazać mi błąd?

Suweren: Przedział wyżej jest od <0,π> a nie od <0, 2π>, pomyliłem się.