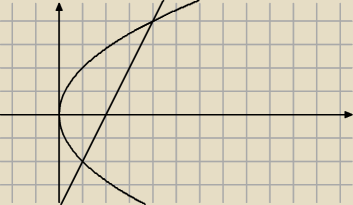
pole obszaru ograniczonego funkcjami kfiatek: Oblicz pole obszaru ograniczonego parabolą y²=4x i prostą y=2x−4. Narysowałam sobie już wykres, tylko mam problem z tym jak podstawić te funkcje do wzoru P=∫g(x)f(x)dx (calka oczywiscie w odpowiednich granicach, ktorych tez nie potrafie ustalic ), bo pojawia sie tu y², a nie x² i wszystko psuje Mam odwrocic uklad wspolrzednych? Moze w ten sposob? I wowczas mialabym: parabole x=¹₄y² prosta x=¹₂y+2 i granice ustalilabym na NOWEJ OX? Prosze o podpowiedz

Krzysiek: możesz podzielić obszar na dwa obszary dla x∊[0,2] i x∊[2,4] albo tak jak piszesz całkować po 'y' i wtedy y∊[−2,4]

kfiatek: czyli generalnie przy pomocy odwrocenia osi da sie to zrobic ale mimo tego, jezeli moge, chcilabym sie dowiedziec, jak mialabym liczyc przy normalnym ustawieniu OX i OY. wiem, ze obszar trzeba podzielic tak jak napisales: x∊[0,2] i x∊[2,4]. tylko co zrobic z tym y²=4x? bo to rownanie ma dwa rozwiazania: y=2√x i y=−2√x. ktore z nich mialabym wstawic do calki? da sie to ustalic jednoznacznie? czy jest to obojetne?

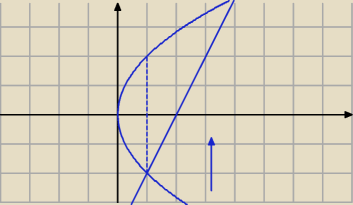
Krzysiek: nic nie musisz odwracać, jak całkuesz po 'x' to wtedy dla x∊[0,1] (wyżej błędnie napisałem) to zgodnie z kierunkiem strzałki na rysunku pierwszą funkcją którą przetniesz to y=−2√x a druga to y=2√x więc masz do policzenia całkę: ∫₀¹∫_−2√x^2√x dydx podobnie dla x∊[1,4] y∊[2x−4,2√x]

kfiatek: ok, juz chyba rozumiem. dzieki