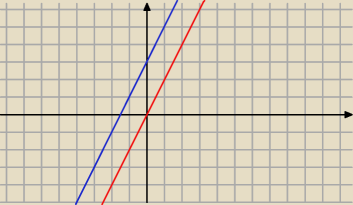
A#3 Lukas: Opisz za pomocą układu nierówności zbiór punktów leżących między prostymi o równaniach y=2x i y=2x+3 3.12 Kiełbasa y≥2x y≤2x+3 czy inaczej ?

razor: y > 2x y < 2x+3

Lukas: Też, właśnie myślałem, że mogą być tylko większe, ale z czego to wynika ?

jakubs: Według mnie, jeżeli leża między prostymi tzn nie należą do tyhc prostych, tylko do przestrznei miedzy nimi

razor: Punkt leżący między prostymi nie należy do tych prostych

Mila: Ostre nierówności połączone spójnikiem "i", bo chodzi o obszar między prostymi. y>2x i y<2x+3

Lukas: ale obszar pomiędzy prostymi to też to co leży na prostej ?

Lukas: ?

Lukas: ?

Lukas: Kiedy te punkty należałby do prostych ?

zawodus: wystarczy zmienić treść zadania i dodać "wraz z tymi prostymi"

Lukas: Nadal nie rozumiem czemu punkty należące do prostych nie są zaliczane do tej przestrzeni ?

Mila: Samochodem jedziesz po szosie, a nie po poboczu. Obszar między prostymi to szosa.

Lukas: Mogę jeszcze kilka zadań ?

Mila: Naturalnie. Może podołam trudom w przerwach meczu.

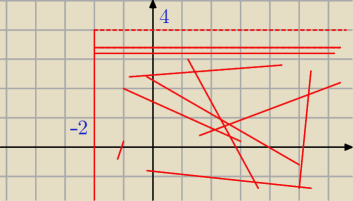
Lukas: Zbiór, którego fragment pokazany jest na rysunku, jest zbiorem punktów płaszczyzny, których współrzędne spełniają układ nierówności z dwiema niewiadomymi. Zapisz ten układ nierówności. x≥−2 y<4 ?

Mila: Dobrze, możesz też przekształcic i mieć zapisane: x+2≥0 i y−4<0 ( tak sie pojawia w testach wyboru).

Lukas: Koło k ma środek S=(2,−1) i promień r =2 Opisz za pomocą nierówności a) koło k (x−2)²+(y+1)²?4 co w miejscu ?

Mila: (x−2)²+(y+1)²≤4 to wynika z definicji koła .

tyu: Lukas robisz jakiś konkretny zbiór pod maturę, czy pracę domową ?

Lukas: Racja b) wnętrze koła k (x−2)²+(y+1)²<4 ? c) zewnętrze koła k ? (x−2)²+(y+1)²>4

Mila: Dobrze. 21:57

Lukas: Maturę pisałem w tym roku. nawet chyba przyzwoicie napisałem bo w abc miałem tylko 1 błąd a otwarte też raczej dobrze, ale na moje studia okazało się, że trzeba pisać R więc uczę się i za rok podchodzę

Lukas: a w c) (x−2)²+(y+1)²≥4 czemu tak nie mogło by być ?

tyu: rozumiem.

Mila: (c) okrąg zaliczamy do koła, a ma być obszar na zewnątrz.

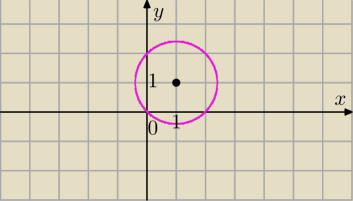
Lukas: Jaki zbiór tworzą wszystkie punkty (x,y) których współrzędne spełniają dane równanie a) x²+y²=2(x+y) x²−2x+y²−2y=0 (x−1)²+(y−1)²=2 To jest równanie okręgu ale jaki zbiór ?

Piotr 10: odejmij stronami równania

Lukas: Jak ja mam tylko jedno równanie x²+y²=2(x+y) reszta to moje przekształcenia.

Mila: Równanie okręgu i masz okrąg . Narysuj i będziesz miał zbiór punktów. S=(1,1) r=√2

Lukas: Wiem, jak to narysować ale jaką podać odp? po prostu okrąg o S=(1,1) r=√2 ?

Mila: Tak jest!

Lukas: b) xy=2

	2
y=
	x

Hiperbola ?

Mila: Tak.

Lukas: To już większość zrobię, tylko jeszcze takie co nie wiem wgl x²=y² co z tym ?

5-latek: ja bym napisal tak: Punkty te tworza zbior wszysktkich punktow rownoodleglych o r=√2 od punktu S(1,1)

Mila: x²−y²=0 (x−y)*(x+y)=0 x−y=0 lub x+y=0 y=x lub y=−x suma prostych.

Lukas: ?

Mila: +

Lukas: Jak opisać ten zbiór ?

Mila: Ostatnia linijka wpisu 23:56, nie miałeś tego w LO?

Lukas: Ja miałem tylko podstawę w szkolę .. x²−y²=0 to wiem, że wzór skr. mnożenia a²−b²⇔(a−b)(a+b)

Lukas: Dziękuję, jutro do tego wrócę

5-latek: Lukas chodzi o ostania linijke tego wpisu jesli oznaczymy y=x przez A i y=−x przez B to z dzialan na zbiorach weimy z esuma zbiorow AUB to zbior zawierajacy wszystkie elementy zbioru A i zbioru B Co jest elementem zbioru A i co jest elementem zbioru B?

Lukas: Wiem, że chodzi o ostatnią linijkę ale to raczej iloczyn a nie suma ? Poczekam z tym do jutra

Mila: x−y=0 lub x+y=0 widzisz spójnik lub ?

Lukas: Tak widzę.

5-latek: Otoz nie iloczyn tylko suma Masz dwa czynniki jeden to (x−y) i drugi (x+y) iloczyn tych dwoch czynnikow =0 gdy (x−y)=0 lub x+y=0 Kluczowym tu jest spojnik lub ktory wlasnie odnosi sie do sumy a nie do iloczynu zbiorow(do iloczynu stosujemy spojnik i

Lukas: Już wszystko rozumiem, tak jak działania na zbiorach. Dziękuję i dobranoc.