Odległość punktu od krzywej mateo: Najmniejsza odległość środka układu współrzędnych do krzywej xy=8... Ktoś pomoże?

5-latek:

	8
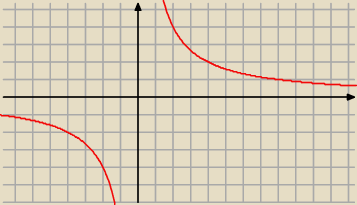
x*y=8 to y=		tak mysle i wykres bedzie taki
	x

pigor: ..., jest to odległość punktu (0,0) od punktu przecięcia się prostej y=x z krzywa xy=8 (hiperbolą),czyli y=x i x²=8 ⇔ |x|=2√2=y ⇒ (x,y)=(2√2,2√2) v (x,y)=(−2√2,−2√2), zatem d_najmn.=2√2*√2 =4 − szukana odległość . ..

mateo: pigor należy Ci się zimny browar!

pigor: ..., no właśnie, dziękuję, idę do lodówki, bo bym ... zapomniał, że coś tam na mnie ...czeka.

mateo: wypij za mnie bo ja nie mogę!

Toskan: A dlaczego krzywa y=x? Ja bym to zrobił tak.

	8
Weźmy dowolny punkt należący do hiperboli. Px0 = (x0,		).
	x0

Szukamy odległości punktu O(0, 0) od punktu P. |OP| = √x²₀ + 64/x²₀ Odległość będzie najmniejsza, gdy wartość funkcji

	64
h(x) = x2 +		będzie najmniejsza.
	x2

Po zbadaniu przebiegu zmienności funkcji h odczytujemy, że funkcja h przyjmuje wartość najmniejszą równą 16 dla argumentów x∊(−2√2, 2√2)

Toskan: x∊{−2√2, 2√2}