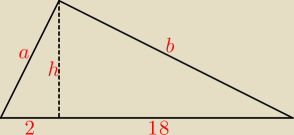
trójkąt prostokątny, obliczyć pole jojek123: Wysokość trójkąta prostokątnego poprowadzona na przeciwprostokątną podzieliła ją na odcinki długości 18 cm i 2 cm. Oblicz: a) pole tego trójkąta, b) promień okręgu opisanego na tym trójkącie, c) promień okręgu wpisanego w ten tójkąt.

Darth Mazut: a) Układ równań: 2² + h² = a² 18² + h² = b² a²+b² = 20², gdzie h − wysokość poprowadzona na przeciwprostokątną, a i b boki trójkąta b) przeciwprostokątna jest średnicą okręgu opisanego

jojek123: Dzięki wielkie, nie pomyślałem o tym sposobie.

jolka: h = √2*18 = 6, a = √36 − 4 = 4√2, b = √36 + 324 = 6√10,

	2 + 18		1
R =		= 10, r =		(a + b + 20}
	2		2

Darth Mazut: r wpisanego wyszedł mi 6√10 − 18

Darth Mazut: 36 + 4 = a² <==> a = 2√10 sprawdź to

Metis: Lub z wysokości trójkąta prostokątnego: h=√ c1*c2 Gdzie c1 i c2 to odcinki na które została podzielona przeciwprostokątna U cb c1= 18 c2 = 2 Podstawiasz otrzymujesz wysokość. I liczysz z podstawowego wzoru pole : a*h /2 , gdzie a to twoja przeciwprostokątna − 18+2 a− h wysokość którą wyprowadziłeś.