geometria analityczna
ShawnMichaels: A (3,4) B (−3,2) C (0,3)
Wyznacz środek odcinka AB oraz podaj równanie symetralnej.
Środek to tam wiadomo ze wzoru, ale jak zapisać te równanie symetralnej? Wiem, że symetralna to
prosta prostopadła do danego odcinka i przechodząca przez jego środek.
11 cze 22:49
ICSP: Proste są prostopadłe gdy iloczyn ich współczynników kierunkowych jest równy −1
Czyli na razie musisz wyznaczyć równanie prostej AB
11 cze 22:50
ShawnMichaels: y = ax + b
4 = 3a + b
2 = −3a + b
?
11 cze 22:57
ICSP: To jeden ze sposobów.
11 cze 22:59
bezendu:
Równanie prostej do współczynnika kierunkowego
11 cze 23:02
ShawnMichaels: Czyli a = 13, środek AB = (0,3)
y = 13x+b
Co dalej?
11 cze 23:20
ShawnMichaels: Wyliczyłem, że b = 4
y = 13x + 4
a * a1 = − 1
a1 = −3
Dobrze myślę?
11 cze 23:25
ICSP: Symetralna jest prostopadła do prostej AB, zatem z warunku prostopadłości prostych dostajesz
współczynnik kierunkowy symetralnej.
Masz :
− współczynnik kierunkowy symetralnej
− punkt przez który ona przechodzi
Możesz zapisać jej równanie.
11 cze 23:26
ShawnMichaels: Ok już ogarniam. Dzięki
11 cze 23:30
ICSP: Mogę Ci jeszcze pokazać inną metodę szukania symetralnej odcinka
11 cze 23:39
bezendu:
A (3,4) B (−3,2)
√(x−3)2+(y−4)2=√(x+3)2+(y−2)2 /2
(x−3)2+(y−4)2=(x+3)2+(y−2)2
11 cze 23:42
Eta:
11 cze 23:46
bezendu:
Dla kogo ?
11 cze 23:47
Eta:
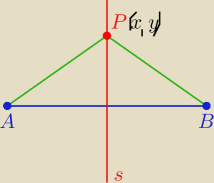
s: |AP|=|BP| dalej tak, jak napisał
bezendu
11 cze 23:50
Eta:
No jasne,że dla
bezendu 
11 cze 23:51
bezendu:
Dziękuję
11 cze 23:52