A#2
Lukas:
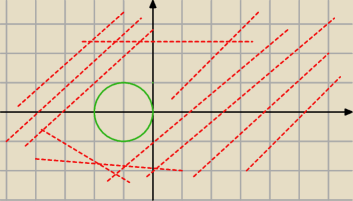
Zaznacz w układzie wsp zbIór
a) A={(x,y):x
2+y
2+2x>0}
a) (x+1)
2+y
2=1
dobry obszar zaznaczyłem ?
11 cze 21:53
Marcin: Tak
11 cze 22:16
Lukas:
Na pewno ? 100% ?
11 cze 22:17
Marcin: (x+1)
2+y
2>1 <− może z tą małą różnicą, że ma to być nierówność
11 cze 22:22
Lukas:
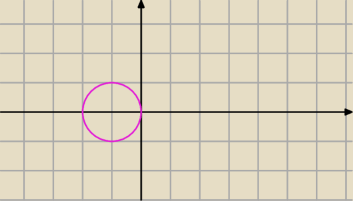
A no tak
(x+1)
2+y
2>1
i ta 1 to nie wiadomo czy x=1 czy y=1 ?
11 cze 22:25
Marcin: Chodzi Ci o jedynkę po prawej stronie? Przecież to jest promień do kwadratu
11 cze 22:27
Lukas:
Ale to jest nierówność ? Wiem, że jedynka ale równanie okręgu ma być większe od 1 ?
11 cze 22:29
Marcin: Szukasz punktów, gdzie okrąg o środku (−1;0), ma promień większy od 1 (to co sam zaznaczyłeś).
Tyyle.
11 cze 22:31
Lukas: Dzięki choć wydaję się mi to jeszcze dziwne..
11 cze 22:45
11 cze 22:47
Lukas:
Oprócz koła ale tam jest >1 ?
11 cze 22:54
Marcin: Nie rozumiem..
Nie wiesz skąd wzięła się 1?
11 cze 23:15
Lukas:
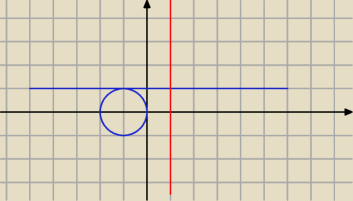
Rozumiem:
ale graficznie powinno się tą jedynkę zaznaczyć ?
11 cze 23:16
Marcin: Nie. Przecież masz >1
11 cze 23:22
Lukas:
Większe od jedynki ale na osi oy czy ox ?
11 cze 23:22
Mila:
1) Równanie :
(x+1)
2+y
2=1 opisuje zbiór wszystkich punktów należących do okręgu o środku
S=(−1,0) i promieniu 1
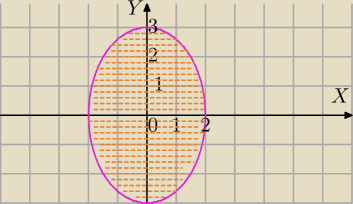
2) Nierówność :
(x+1)
2+y
2≤1 opisuje obszar wewnątrz tego okręgu łącznie z okręgiem , czyli koło.
3) nierówność:
(x+1)
2+y
2>1 opisuje obszar na zewnątrz koła o promieniu r=1 i środku S=(−1,0).
Równanie :
| x2 | | y2 | |
| + |
| =1 opisuje krzywą stożkową− elipsę. |
| 4 | | 9 | |
Nierówność :
| x2 | | y2 | |
| + |
| ≤1 opisuje obszar wewnątrz tej elipsy. |
| 4 | | 9 | |
11 cze 23:33
Lukas:
Ale tam mam, że są większe od 1 ? Więc jak to narysować ?
11 cze 23:35
Mila:
11 cze 23:36
Mila:
Przeczytaj punkt (3). Mam Ci narysować?
11 cze 23:37
Lukas:
Tak, niby wiem, że to jest koła ale ta 1 nie daję mi spokoju...
11 cze 23:39
Mila:
Przecież musisz podać środek i promień koła, aby go jednoznacznie umieścić na płaszczyźnie z
układem współrzędnych.
11 cze 23:41
Lukas:
Nie rysuję się tej 1 (pomocniczo ) ?
11 cze 23:42
Marcin: Ale co Ty chcesz od tej jedynki?
Przecież to jest promień. Nie wiem dokładnie o co Ci chodzi
w: "Większe od jedynki ale na osi oy czy ox ?"
11 cze 23:43
Marcin: Ty chyba dalej nie rozumiesz, że ta 1 to jest promień. Przecież to równianie okręgu.
11 cze 23:44
Mila:
No dwa razy chcesz tę jedynkę wykorzystać?
Rysujesz koło o środku (−1,0) i promieniu r=1.
Koniec. Skąd weźmiesz drugą jedynkę.
(x+1)2+y2=1
Z lewej strony masz równanie krzywej, nie masz tu wzoru funkcji.
11 cze 23:46
Lukas:
Takie buty.
23:36 to nierówność 4 ?
11 cze 23:51
Mila:
Tak, obszar wewnątrz elipsy, tu też po lewej stronie nie masz wzoru funkcji.
11 cze 23:56
Lukas:
Dziękuję a taki przykład jeszcze nie daję mi spokoju ?
polecenie to samo A....xy≤0
11 cze 23:58
Marcin: kiedy iloczyn dwóch liczb jest ≤0
12 cze 00:09
Lukas: ?
12 cze 20:31
Lukas:
Ale nie da się namalować xy ? co innego y=x, ale xy..
12 cze 21:11
uka:
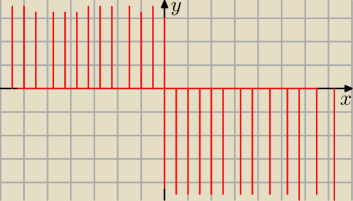xy≤0 ⇔(x≤0 ⋀ y≥0) v (x≥0 ⋀ y≤0 ) x,y ∊R
12 cze 21:28
Lukas: Dzięki.
12 cze 21:30
pigor: ..., ależ da się , bo
xy≤ 0 (iloczyn x i y jest niedodatni) ⇔ (x≤ 0 ⋀ y ≥0)
v (x ≥0 ⋀ y≤ 0) jest to
alternatywa koniunkcji półpłaszczyzn, czyli tu :
na płaszczyźnie z układem XOY jest suma mnogościowa punktów ćwiartki II i IV,
wraz z ich "brzegiem " i punktem (0,0) .
−−−−−−−−−−−−−−−−−−−−−−−−−−−
p.s..
przepraszam, że nie wytrzymałem i ...
pomagam tu i teraz ...
12 cze 21:32
pigor: ... O
spóźniłem się ; jak zwykle
12 cze 21:34
Lukas:
Nie powinno być tak ?
12 cze 21:37
uka:
12 cze 21:43
Lukas:
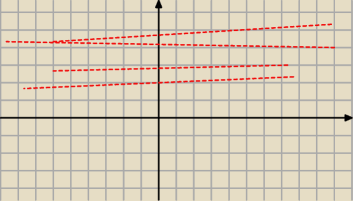
Ale x≥0 jest
Proszę o wytłumaczenie.
12 cze 21:52
pigor: hmm... , no to weź sobie np. punkt (x,y)=(3,4)∊I ćw., to i 3*4=12
, czy jest iloczyn x*y <0
, albo (x,y)=(−2,−3)∊III ćw, to ... xy= ...
12 cze 21:52
uka:
Masz dwie"diagnozy"
pigora i moją i...... nadal "boli Cię",że nie jest tak,
jak Ty myślisz?( czyli błędnie)
Teraz oglądam
12 cze 21:55
Lukas:
Chyba że to jest koniunkcja x≥0 i y≤0 wtedy to tak
12 cze 21:55
Lukas:
Tylko pytam się o wytłumaczenie a nie docinki
I nic mnie nie boli a Ciebie ?
12 cze 21:57
Mila:
Koniunkcja , zobacz, jest znaczek ∧ w zapisach pigora 21:32
12 cze 21:59
Lukas:
Dziękuję Mila
właśnie już zrozumiałem
12 cze 22:00
pigor: ...,
. dobre, cóż ten typ tak ...
MA i ...już
12 cze 22:26