podobieństwo trójkątów w trapezie Ilona: W trapezie ABCD podstawy mają długość AB=a i CD=b. Punkt E jest punktem przecięcia przekątnych trapezu. Oblicz stosunek pól trójkątów AED i ABE. Nie mam pojęcia jak wpleść długość b w tym zadaniu do prawdopodobnie podobieństwa. Zadanie potrrzebne mi na jutro. Dzięki.

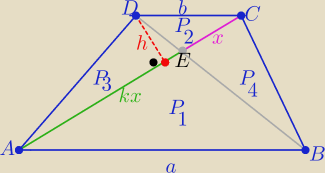
Eta: P₁=P(ABE), P₂=P(DEC) , P₃=P(AED)

	a
Trójkąty ABE i DEC są podobne w skali k=		. k>0
	b

	P1
to:		=k2 ⇒ P1=k2*P2
	P2

	kx*h		x*h
P3=		, P2=		⇒ P3= k*P2
	2		2

P3		k*P2		1		b
	=		=		=
P1		k2*P2		k		a

dyzio: ΔABE ~ ΔCDE (kkk)

ABE		a
	= (		)2
CDE		b

	AED		ED		b
zatem		=		=
	ABE		BE		a

Ilona: Dzięki wielkie − jesteście