Kilka pytan do tego przykładu. lil: Kilka pytan do tego przykładu. http://www.zadania.info/d36/131055 Jak pozbyto siętego pierwsiatka z dwóch Co potem się stało z tą 2 gdy rozpatrzono przypadki wartości bezwzględenej i wyszłoi 0 i 2? Skąd taka odpowiedź? Uczę się do poprawki. Błagam o odpowiedź/

kochanus_niepospolitus:

coś		coś innego
	≤		<=> coś ≤ coś innego (jeżeli ów stała jest > 0)
stała		stała

albo inaczej ... po lewej stronie w mianowniku masz √1+1 ... a to przecie √2 stąd masz takie same mianowniki ... możesz przemnożyć tą nierówność przez √2 i już ułamki 'znikają'

kochanus_niepospolitus: tak ... później przypadki zostały rozpatrzone

lil: Super wytłumaczenie. Dziękuję! Jednak nie rozumiem czemu gdzieś zniknęła ta 2? Bo najpierw jest rozpatrzony przypadek 0 i 2, a później zostaje nam tylko zero linijkę niżej.

lil: Może mi ktoś powiedzieć dlaczego jest taka odpowiedź w tym zadaniu bo nie rozumiem. Jak sinusoida może być miedzy <0,2>? Przecież ona moze byc tylko między <−1,1> Błagam!

J: A dlaczego nie może być ? przedział <0,2> zawiera przedział <0,1> i tam jest ta część sinusoidy. Zapis: 0 ≤ sinx ≤ 2 ... wynikał z przekształcenia nierówności.

lil: A mógłbyś/aś mi to pokazać na rysunku? Proszę !

lil: Bo ja to rozumiem tak, że zbiór rozwiązań jest od <−1,1>, a dziedzina jeśli ma być od <0,2> to w którym momencie jest to dwa? Przy 2π czy ³₂π

lil: Według tego wykresu https://matematykaszkolna.pl/strona/426.gif 2 jest przy ²₃π. Więcz czemu jest taka odpowiedź?

J: Rozwiązaniem zadania jest warunek : 0 ≤ sinx ≤ 1, czyli wszystkie te przedziały,gdzie sinx jest nieujemny. Pierwszy przedział to <0,π> (popatrz na wykres) ... i powtarza się co 2kπ , czyli rozwiązanie: x ∊ <0+2kπ, π + 2kπ>

lil: Ale przecież jak rozwiązujemy to mamy 0 ≤ sinx ≤ 2

J: Ale sinx musi należeć do przedziału :<−1,1> .... i w tym zadaniu musi być w przedziale: <0,1>

J: Rozwiązaniem nierówności: − 15 ≤ sinx ≤ 150 jest to samo co : −1 ≤ sinx ≤ 1

lil: Czyli ta 2 która jest w trzeciej linijce od dołu nie ma znaczenia bo i tak msuze popatrzeć na na przedział do 1?

lil: Kurde dalej nie rozumiem.

J: Oczywiście.

lil: No ale dalej nie rozumie tego, że skoro mam popatrzeć na 1https://matematykaszkolna.pl/strona/426.gif to czemu odpowiedź nie jest od <2kπ, ^π₂ +2kπ>

J: Przeczytaj uważnie post 16:15 , szukamy przedziałow , gdzie sinx jest nieujemny ( sinx ≥ 0 )

lil: Czyli mam patrzeć na oś OY, a nie na oś OX i mimo że jest między <0,2> muszę i tak patrzeć do 1. Chyba już zaczynam pomału rozumieć.

J: Na osi OX szukasz tych przedziałów domkniętych, gdzie sinusoida jest nad osią OX.

lil: No to skoro szukam na osi OX to czemu nie patrzę tylko do tej dwójki która jest na tym obrazku przed π a za ^π₂

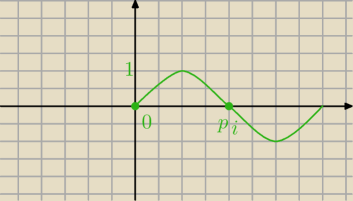
J: Popatrz na rysunek , sinusoida jest nad osią OX dla x <0,π> i to się powtarza co 2kπ (360^o)

lil: To ostatnie pytanie. Czyli jak mam linijkę 0 ≤ sinx ≤ 2 0 ≤ sinx to znika ta dwójka bo zbiór wartości może byc tylko między <−1,1> tak?

J: Tak.

lil: Super! Wielkie dzięki! Trochę cię wymęczyłam. Przepraszam!